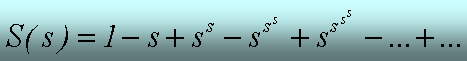|
Identities involving binomial-coefficients,
|
|
A Power-tower-problem
Documentation of matrixmultiplication in the neighbourhood of s=1/exp(1),
where infinities would occur in intermediate terms
(for a description see: powertowerproblem.pdf)
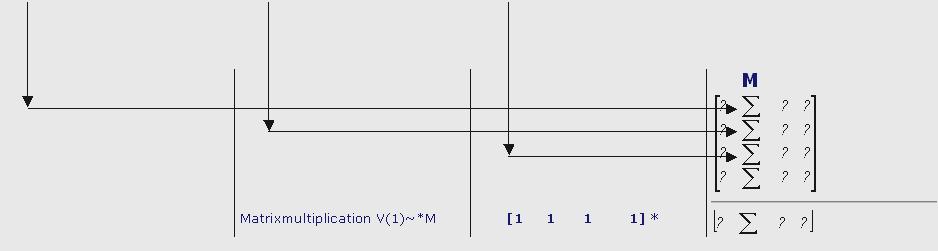
Each column of the following tables represents the additive terms, which occur, if I matrix-multiply one row with one column in aproduct of two matrices. From each column-sum one entry in the column 1 in matrix M is constructed; all entries of this column in M form the sum for the representation of S(s) = 1 - s + s^s - s^s^s + ....
The result has to be computed by first summing the columns.
Except of the leading two terms of the first left columns the sums behave very good. The high leading terms cancel and the result for each column is dominantly determined by the nearly cannceling sum of the two leading entries.
Second, the column-sums must be added, which is then a relatively smooth matter even in the very near region about the point, which causes singularities in the computation.
The tables are excerpts of dim=64 matrices, where also the entries besides the top-left 2x2-square stabilize with the approximation to the terms for the function at the critical point.
Additional remark: it seems, as if the sum S0 of the first column is just the negative value for the result S, so actualy only that column must be added to get the final result-value.
Approximation from above
s = 1/exp(1)+0.001
|
0 |
. |
. |
. |
|
-184.1896074776525 |
368.3792149553049 |
. |
. |
|
182.9436646854058 |
-365.3900366256707 |
-0.4972927451409081 |
. |
|
0.02668116372507938 |
0.001789356478404914 |
-0.1654599223837150 |
0.1103082384551513 |
|
0.04783753530689442 |
-0.1494527476022097 |
0.1988660847661194 |
-0.1822146537311914 |
|
-0.02100271628208042 |
0.06816730602625324 |
-0.09056939550202863 |
0.06623394600548387 |
|
0.001302512017450061 |
-0.008795419731917340 |
0.02652567782830224 |
-0.04722081108469935 |
|
-0.003685435242448678 |
0.01854076597252980 |
-0.04553549407927089 |
0.07251094229879511 |
|
0.0004242710941352813 |
-0.002134788081959128 |
0.005001766193481713 |
-0.006908465097640496 |
|
-0.00007390401103214041 |
0.0005424352212128997 |
-0.001954999802240941 |
0.004523965179696778 |
|
0.000004181134805687424 |
-0.00003028429494405708 |
0.0001080000918308930 |
-0.0002479871420892002 |
|
-0.000001400007476206085 |
0.000009126534186219818 |
-0.00002673644898971030 |
0.00004090732706741211 |
|
... |
... |
... |
... |
|
|
|
|
|
|
|
|||
In the sum Σ, occuring from V(1)~ * M in the second column of the result is the interesting result S = f(s)
Better approximations:
s = 1/exp(1)+0.0001
|
0 |
. |
. |
. |
|
-1839.647194532576 |
3679.294389065153 |
. |
. |
|
1838.397602071757 |
-3676.295475860918 |
-0.4997282825961161 |
. |
|
0.02766714190653941 |
0.0001809890644326949 |
-0.1665458678371510 |
0.1110305949596394 |
|
0.04901240228778375 |
-0.1533993160824288 |
0.2044907439505548 |
-0.1874417379479159 |
|
-0.02175233798377561 |
0.07074461450867856 |
-0.09429302109675247 |
0.06936512018671628 |
|
0.001248280721468750 |
-0.008604496515357811 |
0.02625846389813101 |
-0.04704723978013702 |
|
-0.003707960245963034 |
0.01868860404119574 |
-0.04598349495393260 |
0.07334292509278798 |
|
0.0004465445379198679 |
-0.002255492663576624 |
0.005313161595532777 |
-0.007402369912644593 |
|
-0.00007605732493294964 |
0.0005611031592435205 |
-0.002031317947529616 |
0.004718429277811968 |
|
0.000006571230507649609 |
-0.00004768952443873597 |
0.0001704045864499089 |
-0.0003920391162226768 |
|
-0.000001632857950695801 |
0.00001077204159982626 |
-0.00003220826060299780 |
0.00005173096375013639 |
s = 1/exp(1)+0.00001
|
0 |
. |
. |
. |
|
-18394.22205743951 |
36788.44411487903 |
. |
. |
|
18392.97209821171 |
-36785.44422360513 |
-0.4999728182900169 |
. |
|
0.02776670438630083 |
0.00001811958019663983 |
-0.1666545855509429 |
0.1111030571981446 |
|
0.04913198789228077 |
-0.1538013937897740 |
0.2050643445060255 |
-0.1879748361790386 |
|
-0.02182902754653513 |
0.07100848394028226 |
-0.09467465420893245 |
0.06968654751494943 |
|
0.001242869708798918 |
-0.008585535933662890 |
0.02623227145551232 |
-0.04703100631054961 |
|
-0.003710375297457230 |
0.01870424092356531 |
-0.04603048794775549 |
0.07342975784462057 |
|
0.0004488320436847083 |
-0.002267906383190432 |
0.005345241083779504 |
-0.007453362071235202 |
|
-0.00007623856763362795 |
0.0005627332049798308 |
-0.002038140977151129 |
0.004736096450462607 |
|
0.000006780377520727165 |
-0.00004921703001871117 |
0.0001758971154309515 |
-0.0004047537795079106 |
|
-0.000001657384693752924 |
0.00001094629085532064 |
-0.00003279203219645760 |
0.00005290000410265011 |
s = 1/exp(1)+0.0000001
|
0 |
. |
. |
. |
|
-1839397.455857200 |
3678794.911714401 |
. |
. |
|
1839396.205857608 |
-3678791.911715488 |
-0.4999997281719280 |
. |
|
0.02777766703307156 |
0.000000181218558 |
-0.1666665458541546 |
0.1111110305694528 |
|
0.04914516600900403 |
-0.1538457061615343 |
0.2051275663958011 |
-0.1880335943978930 |
|
-0.02183748294436158 |
0.07103757905760699 |
-0.09471673882065796 |
0.06972199866327808 |
|
0.001242274603712257 |
-0.008583451606960474 |
0.02622939589761666 |
-0.04702923275455186 |
|
-0.003710642754012892 |
0.01870597045353450 |
-0.04603568158113433 |
0.07343934996598768 |
|
0.0004490843502746740 |
-0.002269275779867336 |
0.005348780479676852 |
-0.007458989374231436 |
|
-0.00007625819063403634 |
0.0005629103472735577 |
-0.002038884180155027 |
0.004738023846524048 |
|
0.000006803118126976280 |
-0.00004938316434201603 |
0.0001764946644815707 |
-0.0004061374352088517 |
|
-0.000001660096754012488 |
0.00001096556868295206 |
-0.00003285666419280056 |
0.00005302958822060768 |
s = 1/exp(1)+0.0000001 dim = 78
|
0 |
. |
. |
. |
|
-1839397.45586 |
3678794.91171 |
. |
. |
|
1839396.20586 |
-3678791.91172 |
-0.499999728172 |
. |
|
0.0277776670331 |
0.000000181218558682 |
-0.166666545854 |
0.111111030569 |
|
0.0491451660090 |
-0.153845706162 |
0.205127566396 |
-0.188033594398 |
|
-0.0218374829444 |
0.0710375790576 |
-0.0947167388207 |
0.0697219986633 |
|
0.00124227460371 |
-0.00858345160696 |
0.0262293958976 |
-0.0470292327546 |
|
-0.00371064275401 |
0.0187059704535 |
-0.0460356815811 |
0.0734393499660 |
|
0.000449084350275 |
-0.00226927577987 |
0.00534878047968 |
-0.00745898937423 |
|
-0.0000762581906340 |
0.000562910347274 |
-0.00203888418016 |
0.00473802384652 |
|
0.00000680311812698 |
-0.0000493831643420 |
0.000176494664482 |
-0.000406137435209 |
|
-0.00000166009675401 |
0.0000109655686830 |
-0.0000328566641928 |
0.0000530295882206 |
Approximation from below
s = 1/exp(1)-0.00001
|
0 |
. |
. |
. |
|
18393.72205743948 |
-36787.44411487897 |
. |
. |
|
-18394.97209821574 |
36790.44422361541 |
-0.5000271839266999 |
. |
|
0.02778885334948239 |
-0.00001812417783156476 |
-0.1666787480560592 |
0.1111191655349260 |
|
0.04915861520015104 |
-0.1538909308865261 |
0.2051920912463972 |
-0.1880935636802537 |
|
-0.02184611315896496 |
0.07106727617666840 |
-0.09475969511328736 |
0.06975818526801267 |
|
0.001241667497389819 |
-0.008581325443019169 |
0.02622646338787375 |
-0.04702742583811662 |
|
-0.003710915981494334 |
0.01870773685846845 |
-0.04604098512243409 |
0.07344914414762636 |
|
0.0004493418933500680 |
-0.002270673636896916 |
0.005352393559179149 |
-0.007464734079187612 |
|
-0.00007627814716673758 |
0.0005630906349544153 |
-0.002039640930253399 |
0.004739986982003151 |
|
0.000006826265105931587 |
-0.00004955227729447474 |
0.0001771029619064992 |
-0.0004075460583757432 |
|
-0.000001662866494694891 |
0.00001098525857540021 |
-0.00003292268733243007 |
0.00005316199296922276 |
Differences of terms
in matrixmultiplication when approximatiaten from below and from above
for computations of f(s0- 0.0000000001) and f(s0+ 0.0000000001) dim=78
sums
|
0 |
. |
. |
. |
. |
. |
|
-0.250000000000000 |
0.500000000000000 |
. |
. |
. |
. |
|
-1.000000000000000 |
2.500000000000000 |
0.000000000543656 |
. |
. |
. |
differences
|
-2.21489630E-10 |
0.000000000362430 |
0.000000000241625 |
-1.61083367612E-10 |
. |
. |
|
-0.0000000002662 |
0.000000000895370 |
-0.000000001277467 |
0.000000001187274 |
-0.000000000272632 |
. |
|
1.70856116E-10 |
-0.000000000587922 |
0.000000000850409 |
-0.000000000716377 |
7.39583027761E-11 |
3.82202906E-11 |
|
1.20221135E-11 |
-4.21049039E-11 |
5.80806712E-11 |
-3.58047174E-11 |
-1.00420636E-11 |
8.20609283E-12 |
|
5.40684042E-12 |
-3.49593488E-11 |
1.04971745E-10 |
-1.93863026E-10 |
0.000000003112 |
-1.82357652E-10 |
|
-5.09849638E-12 |
2.76725354E-11 |
-7.15247494E-11 |
1.13720071E-10 |
-1.11236244E-10 |
5.57952417E-11 |
|
3.95794289E-13 |
-3.57429225E-12 |
1.49995044E-11 |
-3.89052548E-11 |
6.93728436E-11 |
-8.86498660E-11 |
|
-4.58874785E-13 |
3.35246510E-12 |
-1.20584376E-11 |
2.79227270E-11 |
-4.56588171E-11 |
5.49650378E-11 |
|
5.48180024E-14 |
-3.89677143E-13 |
1.30655113E-12 |
-2.61988809E-12 |
3.16016838E-12 |
-1.55008842E-12 |
Partial sums, accumulated by
color
s = 1/exp(1)+0.0000001 dim = 78
|
0 |
. |
. |
. |
... |
|
-1839397.45586 |
3678794.91171 |
. |
. |
|
|
1839396.20586 |
-3678791.91172 |
-0.499999728172 |
. |
|
|
0.0277776670331 |
0.000000181218558682 |
-0.166666545854 |
0.111111030569 |
|
|
0.0491451660090 |
-0.153845706162 |
0.205127566396 |
-0.188033594398 |
|
|
-0.0218374829444 |
0.0710375790576 |
-0.094716738820 |
0.069721998663 |
|
|
0.00124227460371 |
-0.00858345160696 |
0.026229395897 |
-0.047029232754 |
|
|
-0.00371064275401 |
0.0187059704535 |
-0.046035681581 |
0.073439349966 |
|
|
0.000449084350275 |
-0.00226927577987 |
0.005348780479 |
-0.007458989374 |
|
|
-0.0000762581906340 |
0.000562910347274 |
-0.002038884180 |
0.004738023846 |
|
|
0.00000680311812698 |
-0.0000493831643420 |
0.000176494664 |
-0.000406137435 |
|
|
-0.00000166009675401 |
0.0000109655686830 |
-0.000032856664 |
0.000053029588 |
|
|
... |
|
|
|
|
Approximations of partial sums
|
S0.0=S(1..2,0) = sum(k=2,3,tmpMCol[k,1]) |
-> -1.25 |
|
S0.1=S(3..inf,0) = sum(k=4,n,tmpMCol[k,1]) |
~ 0.0530032906978 |
|
S1.0=S(1..2,1) = sum(k=2,3,sum(c=2,n,tmpMCol[k,c])) |
-> 2.5 . |
|
S1.1=S(3..inf,1..inf) =sum(k=4,n,sum(c=2,n,tmpMCol[k,c])) |
~ -0.106006581396 |
|
S0 = S0.0 + S0.1 |
~ -1.19699630156 |
|
S1 = S1.0 + S1.1 |
= - 2* S0 |
All entries in the blue and
read range seem to stabilize to fixed values, and thus their sums, and also
entry E[2,2] in the green area
The four top left entries in
the yellow and green ranges increase. But their sum seems to approximate fixed
values -1.25 and -2*1.25. and because of such convergence of their sums we
possibly get a convergent for the overall result.
The approximation from lower
produces the same sum of all entries, only the row-order of the leading terms
(yellow and green) change. Also some means of entries of lower and upper
approximation (of same precision) suggest, that their common convergent is a
rational number, for instance
E(2,2) -> -½
E(3,2) = -1/6 E(3,3) = 1/9
The overall result with s0
= 1/exp(1) and s = s0 +- eps
of the series
S = 1 - s + s^s - s^s^s + s^s^s^s - ... +...
seems to be (approximated from
above or below)
S
~ 1.25 - 0.05300[32... ~
1.19699[6...
or computed with dim=78, s = 1/exp(1) +- 0.0000000001 in the bounds
1.19699655_674 < S <
1.19699655_725
Gottfried Helms