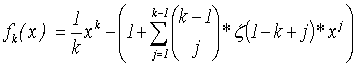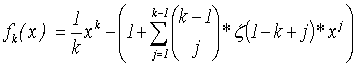| Coefficients of polynomials f_k(x) |
|
|
|
|
|
|
|
|
The summing problem: |
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
is converted by the
well knwon Bernoulli-formula into a polynomial problem. Here the first
parenthese on the rhs is converted into a bernoulli-polynomial in x and the
second parenthese in a binomial-expression acting on the same x. If their
difference is zero at a positive integer x then a solution for the problem is
found. Thus the original problem is restated as a problem of positive integer
zeros of a polynomial in x |
|
|
|
|
Definition of the new
polynomials: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
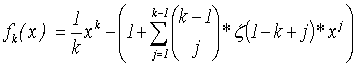
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conjecture / to prove: |
|
|
|
* no positive integer real roots x do
exist for any polynomial f_k(x) k>2 |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
list of unscaled
polynomials f_k(x) |
|
|
|
|
|
|
|
|
|
| K= |
|
| 0 |
f0(x)= |
-1 |
|
| 1 |
f1(x)= |
-1 |
+1 x |
|
|
| 2 |
f2(x)= |
-1 |
-1/2 x |
+1/2 x^2 |
|
|
| 3 |
f3(x)= |
-1 |
-11/6 x |
-1/2 x^2 |
+1/3 x^3 |
|
|
| 4 |
f4(x)= |
-1 |
-3 x |
-11/4 x^2 |
-1/2 x^3 |
+1/4 x^4 |
|
|
| 5 |
f5(x)= |
-1 |
-121/30 x |
-6 x^2 |
-11/3 x^3 |
-1/2 x^4 |
+1/5 x^5 |
|
|
| 6 |
f6(x)= |
-1 |
-5 x |
-121/12 x^2 |
-10 x^3 |
-55/12 x^4 |
-1/2 x^5 |
+1/6 x^6 |
|
|
| 7 |
f7(x)= |
-1 |
-251/42 x |
-15 x^2 |
-121/6 x^3 |
-15 x^4 |
-11/2 x^5 |
-1/2 x^6 |
+1/7 x^7 |
|
|
| 8 |
f8(x)= |
-1 |
-7 x |
-251/12 x^2 |
-35 x^3 |
-847/24 x^4 |
-21 x^5 |
-77/12 x^6 |
-1/2 x^7 |
+1/8 x^8 |
|
| ... |
... |
... |
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
list of factorial
row-scaled polynomials F_k(x), coefficients are definitely integer |
|
|
|
|
|
| K= |
|
| 0 |
F0(x)= |
-1 |
|
| 1 |
F1(x)= |
-1 |
+1 x |
|
|
| 2 |
F2(x)= |
-2 |
-1 x |
+1 x^2 |
|
|
| 3 |
F3(x)= |
-6 |
-11 x |
-3 x^2 |
+2 x^3 |
|
|
| 4 |
F4(x)= |
-24 |
-72 x |
-66 x^2 |
-12 x^3 |
+6 x^4 |
|
|
| 5 |
F5(x)= |
-120 |
-484 x |
-720 x^2 |
-440 x^3 |
-60 x^4 |
+24 x^5 |
|
|
| 6 |
F6(x)= |
-720 |
-3600 x |
-7260 x^2 |
-7200 x^3 |
-3300 x^4 |
-360 x^5 |
+120 x^6 |
|
|
| 7 |
F7(x)= |
-5040 |
-30120 x |
-75600 x^2 |
-101640 x^3 |
-75600 x^4 |
-27720 x^5 |
-2520 x^6 |
+720 x^7 |
|
|
| 8 |
F8(x)= |
-40320 |
-282240 x |
-843360 x^2 |
-1411200 x^3 |
-1422960 x^4 |
-846720 x^5 |
-258720 x^6 |
-20160 x^7 |
+5040 x^8 |
|
| ... |
... |
... |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
list of monic polynomials
M_k(x), (f_k(x) rowscaled to have monic polynomials) |
|
|
|
|
|
| K= |
|
| 0 |
M0(x)= |
-1 |
|
| 1 |
M1(x)= |
-1 |
+ x |
|
|
| 2 |
M2(x)= |
-2 |
-1 x |
+ x^2 |
|
|
| 3 |
M3(x)= |
-3 |
-11/2 x |
-3/2 x^2 |
+ x^3 |
|
|
| 4 |
M4(x)= |
-4 |
-12 x |
-11 x^2 |
-2 x^3 |
+ x^4 |
|
|
| 5 |
M5(x)= |
-5 |
-121/6 x |
-30 x^2 |
-55/3 x^3 |
-5/2 x^4 |
+ x^5 |
|
|
| 6 |
M6(x)= |
-6 |
-30 x |
-121/2 x^2 |
-60 x^3 |
-55/2 x^4 |
-3 x^5 |
+ x^6 |
|
|
| 7 |
M7(x)= |
-7 |
-251/6 x |
-105 x^2 |
-847/6 x^3 |
-105 x^4 |
-77/2 x^5 |
-7/2 x^6 |
+ x^7 |
|
|
| 8 |
M8(x)= |
-8 |
-56 x |
-502/3 x^2 |
-280 x^3 |
-847/3 x^4 |
-168 x^5 |
-154/3 x^6 |
-4 x^7 |
+ x^8 |
|
| ... |
... |
... |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
polynomials f_k(x)
evaluated at some positive integers x |
|
|
|
|
|
|
|
|
equivalent conjecture: |
|
|
|
* no zero occurs except the two marked ones |
|
|
|
|
|
|
|
|
|
|
|
| K= |
|
x= 1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| 0 |
f0(x)= |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
| 1 |
f1(x)= |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
| 2 |
f2(x)= |
-1 |
0 |
2 |
5 |
9 |
14 |
20 |
|
| 3 |
f3(x)= |
-3 |
-4 |
-2 |
5 |
19 |
42 |
76 |
|
| 4 |
f4(x)= |
-7 |
-18 |
-28 |
-25 |
9 |
98 |
272 |
|
| 5 |
f5(x)= |
-15 |
-64 |
-158 |
-271 |
-317 |
-126 |
580 |
|
| 6 |
f6(x)= |
-31 |
-210 |
-748 |
-1825 |
-3351 |
-4606 |
-3760 |
|
| 7 |
f7(x)= |
-63 |
-664 |
-3302 |
-10735 |
-26141 |
-50478 |
-77324 |
|
| 8 |
f8(x)= |
-127 |
-2058 |
-14068 |
-59425 |
-183111 |
-446782 |
-896848 |
|
| ... |
... |
... |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
first approach: |
|
|
|
|
|
|
|
|
|
|
|
|
|
can
the polynomials f3(x)...foo(x) (or F3(x)..Foo(x) )be proven to be irreducible
over Z+? |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
second approach: |
|
|
|
|
|
|
|
|
|
|
|
|
|
derive
a proof, that all real roots for f3(x)..foo(x) are irrational, exploiting the
heuristic evidence |
|
|
|
|
for evidence: see page
"real roots..." |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|