(Last update at13.Feb.2011     remark: I changed the use of the symbol U of the previous version to get a clearer distinction between symbols for the function and that for the matrices)

 

Here I consider the formal powerseries for iterates of the function d(x) = exp(x)-1 .

I'll use the notations

                d(x, 1)                   = d(x) = exp(x) – 1
                d(x, h+1)             = d( d(x,1),h)
                d(x, 0)                   = x

I call the number-of-iterations "height" (of the powertower) and use the letter h for that parameter.

For negative integer h we have the iterates of log(1+x):

                d(x,–1)                 = log(1+x)
                d(x,–2)                 = log(1+log(1+x))
                ...

It is possible to define formal powerseries for fractional iterations consistent with the addition of (iteration-) heights:

                d( d(x, h₁), h₂) = d(x, h₁+h₂)

 

A procedure for the computation can be found for instance in L. Comtet. Comtet introduces the self-composition using the Newton-binomial-formula for the formal powerseries.

In this article I simply use the matrix-logarithm of a small modification of the Bell-matrix for the d(x)

 

                Let U₁ the column-vector of coefficients of the formal powerseries for d(x)
                U₁ = column(0,1,1/2!,1/3!,…)

 

                Then let U₀ the column-vector for d(x)⁰  = 1
                U₀ = column(1,0,0,0,…)

                Let U_c the column-vector for the c'th power of d(x)^c  (not the iterate!)
                U_c = column( )

Then let U the matrix of concatenation of all U_c-vectors. U is then the factorially scaled matrix of the Stirling-numbers 2^nd kind, as, for instance defined in [A&S]

 

Matrixoperator U:

Matrix of Stirlingnumbers 2nd kind (the Bell-matrix for d(x))

 

Further, let's define a general type of Vandermondevector

                V(x) = row(1, x, x², x³, …)

With this we can construct the (iterable) matrix-product:

                V(x) * U = V(d(x)) = V(d(x,1))
                V(x) * U² = V(d(x,1))*U  =  V(d(x,2))

                V(x) * U^h = V(d(x,h))

This expression is so far only meant as expression for the formal composition of the powerseries, which we find in the second column of V(d(x,h)). This means, to get that powerseries we need only consider the second column of the h'th power of U, let's write it this way:

                d(x,h) = V(x) * U^h [,1]

 

 

We can get formal powerseries for fractional iterates analoguosly if we can define fractional powers of the matrix U.

Because the matrix has a unit-diagonal the best method to compute a fractional power is to use the matrix-logarithm defined by the mercator-series using U–I as parameter.

                UL = Log( U ) = (U–I) – (U–I)²/2 – (U–I)³/3 + … – …

The argument U–I is nilpotent to any selected truncation size, so that series gives finite expressions for the entries of UL at any finite row/column-index and these evaluate then to exact entries in rational numbers. This allows a meaningful interpretation of that matrix-logarithm.

To compute fractional powers of U we can then similarly use the matrix-exponential

                U^h = Exp( h * Log(U))

And then, as above we get the formal powerseries for the fractional iterate by the second column of the h'th power of U:

                d(x,h) = V(x) * U^h [,1]                   // also valid for all h

For instance, for h=1/2 we get the matrix U^1/2

 

Matrixoperator U1/2:

 

giving the formal powerseries

               

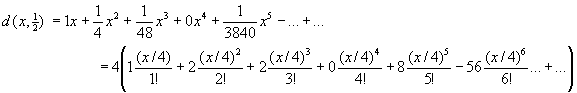
whose coefficients increase strongly such that the radius of convergence of this series is zero.

The first 20 coefficients of that formal powerseries are

                0, 1, 2, 2, 0, 8, -56, 32, 10176, -215808, -78784, 150990912, -3405688576,
                 -139041794560, 10385778676736, 130003936220160, -43016304236761088,
                 526545841919713280, 266085261164348628992, -12347306589339686547456

and it seems, that the above scaling ensures that those coefficients are all integer.

 

 

Because of the convenient properties of the logarithm of the matrix U we can express the coefficients of the powerseries depending on a variable h in terms of polynomials of that h:

                d(x,h)   =  1x
                                + (1/2*h)x²
                               + ( 1/4*h² - 1/12*h) x³
                               + ( 1/8*h³ - 5/48*h² + 1/48*h) x⁴
                               + ( 1/16*h⁴ - 13/144*h³ + 1/24*h² - 1/180*h) x⁵
                               + …

or, attempting to get integer coefficients

               

 

From this we can write the two-parameteric function d(x,h) formally as matrix-product introducing the matrix POLY of coefficients of that polynomials

                d(x,h) = V(x) * POLY * V(h) ~

where the top-left truncation of  POLY looks like

Matrix POLY of coefficients for the two-parametric function d(x,h):

 

For a given height h this means, that we have to multiply POLY with the transpose V(h)~ to get the column-vector U₁ corresponding to U^h[,1] which contains the coefficients for the formal powerseries for the h'th iterate:

                U₁ = U^h[,1] = POLY * V(h)~

and then

                d(x,h) = V(x) * U₁

An eyeball-check gives for h=1 : POLY * V(1)~ for the first few rows:

                1 = 1                                                     row 1 for coefficient at x
                1/2*h = 1/2                                      row 2 for coefficient at x²
                -1/12*h+1/4*h² = 1/6                 row 3 for coefficient at x³
                1/48–5/48+1/8 = 1/24              row 4 for coefficient at x⁴

                … giving coefficients for exp(x)-1

For h=-1 : POLY * V(-1)~ for the first few rows:

                1 = 1                                                     row 1 for coefficient at x
                1/2*h = -1/2                                    row 2 for coefficient at x²
                -1/12*h+1/4*h² = 1/3                 row 3 for coefficient at x³
                -1/48–5/48-1/8 =– 1/4             row 4 for coefficient at x⁴

                … giving coefficients for log(1+x)

 

(truncation to 32 x 12)

 

 

The interesting thing is here, whether we can change order of summation. This is then interesting, if we always assume x=1 in d(x,h).

 

Since each column is associated with one power of the h-parameter, we may sum up each column to have only one term for a powerseries in h.

 

We see, that the sequence of entries along a column diverge after a local minimum and looking at coefficients of higher index it seems that they will grow at least hypergeometrically (like the factorials) .

I constructed a Noerlund-means method of summation which I can apply to the powerseries if I want to estimate the column-sums meaning we apply  x=1 at d(x,h) keeping h variable. That summation is parametrized to sum alternating series of order gamma(k)^1.5 Remark: this is absolutely experimental and no proof for the correct value , for conversion to convergent series and/or regularity of the result is given so far. But because the results and also the intermediate values seem to be reasonable I give here the assumed column-sums in the brown row at the bottom of the table.

 

This would then give a powerseries for d(1,h) in terms of h:

 

                d(1,h) = 1 + 0.4330 h + 0.1758 h² + 0.06852 h³ + ...

 

and for h=1 this should be e - 1 ~ 1.718 ... and this value is good approximated by the row-sum of the last (brown-marked) row.

 

 

A numerical check of

                U₁ = POLY * V(1)
                Approx = Noerlund(0,0) * ^dV(1)* U₁   // we need no acceleration for this because it's simply the exponential-series

showing the convergence of approx_k to the final value:

left the coefficients in U₁, right the Noerlund-summed partial sums

 

U1	Partial sums: Approx:

 

0	0
1.00000000000	1.10803324100
0.500000000000	1.57457355300
0.166666666667	1.69632420459
0.0416666666667	1.71614032126
0.00833333333333	1.71816671191
0.00138888888889	1.71828087196
0.000198412698413	1.71828207238
0.0000248015873016	1.71828183500
0.00000275573192240	1.71828182789
0.000000275573192240	1.71828182845
0.0000000250521083854	1.71828182846
0.00000000208767569879	1.71828182846
1.60590438368E-10	1.71828182846
1.14707455977E-11	1.71828182846
7.64716373182E-13	1.71828182846

 

The same with h-parameter h= 2, so the second-iteration; d(x,2) = exp(exp(x)-1)-1 with x=1

                U²₁ = POLY * V(2)~
                Approx = Noerlund(0,0) * ^dV(1)* U²₁// again we need no acceleration-procedure for this

 

U21	Partial sums: Approx:

 

0	0
1.00000000000	1.60230732254
1.00000000000	2.77868485049
0.833333333333	3.64038609659
0.625000000000	4.13617161436
0.433333333333	4.38997896613
0.281944444444	4.50325607997
0.174007936508	4.54954546855
0.102678571429	4.56656903743
0.0582754629630	4.57238024057
0.0319596009700	4.57420919266
0.0169996091871	4.57474473371
0.00879662406138	4.57489192860
0.00443943225627	4.57492973020
0.00218975755744	4.57493886159
0.00105757104279	4.57494096334
0.000500896018318	4.57494141015
0.000232971039341	4.57494150301
0.000106534988039	4.57494152085
0.0000479488461554	4.57494152405
0.0000212602719146	4.57494152466
0.00000929459892442	4.57494152474
0.00000400953097900	4.57494152476
0.00000170787472022	4.57494152476
0.000000718768664806	4.57494152476
0.000000299047612615	4.57494152476
0.000000123065453419	4.57494152476
0.0000000501169612163	4.57494152476

 

The same with h-parameter h= -1, so the inverse-iteration; giving log(1+x) with x=1:

                U ^-1₁ = POLY * V(-1)~
                Approx = Noerlund(0,0.95) * ^dV(1)* U^-1₁         // we use only small order of the Noerlundtransformation to accelerate convergence

 

U-11	Partial sums: Approx:

 

0	0
1.00000000000	0.444444444444
-0.500000000000	0.592592592593
0.333333333333	0.658436213992
-0.250000000000	0.680384087791
0.200000000000	0.688797439415
-0.166666666667	0.691601889956
0.142857142857	0.692623801540
-0.125000000000	0.692964438735
0.111111111111	0.693085511172
-0.100000000000	0.693125868651
0.0909090909091	0.693140005390
-0.0833333333333	0.693144717637
0.0769230769231	0.693146352716
-0.0714285714286	0.693146897743
0.0666666666667	0.693147085613
-0.0625000000000	0.693147148237
0.0588235294118	0.693147169718
-0.0555555555556	0.693147176879
0.0526315789474	0.693147179326
-0.0500000000000	0.693147180142
0.0476190476190	0.693147180420
-0.0454545454545	0.693147180513
0.0434782608696	0.693147180544
-0.0416666666667	0.693147180555
0.0400000000000	0.693147180558
-0.0384615384615	0.693147180559
0.0370370370370	0.693147180560
-0.0357142857143	0.693147180560
0.0344827586207	0.693147180560
-0.0333333333333	0.693147180560

 

The same with h-parameter h= 1/2, so giving the formal powerseries for the half-iteration, using x=1 

The approximation is very difficult now since we have a divergent series in the terms, whose characteristic is not yet really known, but seems to be more than hypergeometric, so a high order for Noerlund-summation is needed. However, for size = 64 I got an approximation using Eulersummation of order  ord=2.5 which is shown below.

                U^0.5₁ = POLY * V(1/2)
                Approx = Noerlund(0, 2.5) * ^dV(1)* U^0.5₁         // medium order of Noerlundsummation provides convergence – but it is only local

 

U0.51

Partial sums: Approx:

 

0	0
1.00000000000	0.162591050989
0.250000000000	0.373041564566
0.0208333333333	0.576651361395
0.E-810	0.751214327591
0.000260416666667	0.891123237110
-0.0000759548611111	0.998492144926
0.00000155009920635	1.07840852624
0.0000154041108631	1.13654884139
-0.00000907453910384	1.17810073526
-0.0000000828199706170	1.20737494332
0.00000360740727676	1.22775702511
-0.00000169514972633	1.24180758666
-0.00000133089916348	1.25141142987
0.00000177521444910	1.25792762288
0.000000370353976658	1.26232035257
-0.00000191475684776	1.26526469485
0.000000344673434042	1.26722815289
0.00000241913411616	1.26853149270
-0.00000147705874041	1.26939305279
-0.00000360462602023	1.26996042399
0.00000426030599723	1.27033276648
0.00000619401781838	1.27057634173
-0.0000126252925336	1.27073521306
-0.0000117360887110	1.27083855431
0.0000413952285774	1.27090560466
0.0000222030302120	1.27094900588
-0.000153108566769	1.27097703715
-0.0000278327871472	1.27099510405
0.000641018661899	1.27100672598
-0.000111307516319	1.27101418835
-0.00303026666274	1.27101897160
0.00167666962999	1.27102203256
0.0160951154545	1.27102398833
-0.0157084159784	1.27102523611
-0.0954804645039	1.27102603109
0.139489606827	1.27102653689
0.628520649401	1.27102685831
-1.27694165810	1.27102706231
-4.55956399021	1.27102719163
12.4027724564	1.27102727353
36.1854546816	1.27102732533
-129.305594720	1.27102735806
-311.608441223	1.27102737873
1453.71643376	1.27102739177
2883.75499733	1.27102739998
-17648.6056027	1.27102740515
-28323.2666121	1.27102740840
231312.842070	1.27102741045
289837.706925	1.27102741173
-3269335.96562	1.27102741254
-2992168.60724	1.27102741304
49750634.1587	1.27102741336
28980063.0330	1.27102741356
-813616473.772	1.27102741368
-201961594.949	1.27102741376
14271686431.9	1.27102741381
-1325490857.72	1.27102741384
-267978508283.	1.27102741386
119319788076.	1.27102741387
5.37563669599E12	1.27102741388
-4.37013046468E12	1.27102741388
-1.14977800862E14	1.27102741388
1.37951986894E14	1.27102741388

 

But using more terms it is obvious that that convergence is only local; So I used an experimental stronger parametrization of the Noerlund-summation (in my implementation with two parameters), nonetheless apparently arriving at the same value

                Approx = Noerlund(1.4, 1.3) * ^dV(1)* U^0.5₁     // we need Noerlund-summation for this because series is strongly diverging

Using 256 terms we find the following approximation :

 

U0.51

Partial sums: Approx:

 

0	0	0
1	1.00000000000	0.4166666666666666666666667
2	0.250000000000	0.6802187646414115767312961
3	0.0208333333333	0.8543367076839841850527931
4	1.063167461E-204	0.9728122533370859110058801
5	0.000260416666667	1.055158890718194379537863
6	-0.0000759548611111	1.113322049145836683676599
7	0.00000155009920635	1.154927026644590189403069
8	0.0000154041108631	1.184995099232425260962484
9	-0.00000907453910384	1.206912382008609448210350
10	-0.0000000828199706170	1.223005413341123686437128
11	0.00000360740727676	1.234896974845728865717737
12	-0.00000169514972633	1.243733093659537186974143
13	-0.00000133089916348	1.250331573819650138051143
14	0.00000177521444910	1.255281207630202865239360
15	0.000000370353976658	1.259009183115809527489827
16	-0.00000191475684776	1.261827541981969525892891
17	0.000000344673434042	1.263965589964040800596140
18	0.00000241913411616	1.265592744460861863146730
19	-0.00000147705874041	1.266834787928400056087080
20	-0.00000360462602023	1.267785523004340843822270
21	0.00000426030599723	1.268515189788157734675139
22	0.00000619401781838	1.269076583543275748684661
23	-0.0000126252925336	1.269509526672548941751353
24	-0.0000117360887110	1.269844154811896911030546
25	0.0000413952285774	1.270103343096363738965483
26	0.0000222030302120	1.270304505488932369876442
27	-0.000153108566769	1.270460934623827685972399
28	-0.0000278327871472	1.270582803292161357418455
29	0.000641018661899	1.270677915673107836555729
30	-0.000111307516319	1.270752272718673998185568
31	-0.00303026666274	1.270810498998789451747707
32	0.00167666962999	1.270856165904167737114013
33	0.0160951154545	1.270892037054775901782266
34	-0.0157084159784	1.270920255131584852660284
35	-0.0954804645039	1.270942484470710617007680
36	0.139489606827	1.270960020154843030156470
37	0.628520649401	1.270973871664026359126703
38	-1.27694165810	1.270984827158658745978229
39	-4.55956399021	1.270993502982183114841320
40	12.4027724564	1.271000381858227299430625
41	36.1854546816	1.271005842420900556793057
42	-129.305594720	1.271010182086980195864213
…	…	…
242	1.99391580834E202	1.271027413889951521419677
243	-1.89349634501E202	1.271027413889951521420391
244	-7.29686595931E204	1.271027413889951521421002
245	9.45085000863E204	1.271027413889951521421524
246	2.71412390180E207	1.271027413889951521421972
247	-4.46257691886E207	1.271027413889951521422355
248	-1.02596030513E210	1.271027413889951521422683
249	2.04869812900E210	1.271027413889951521422964
250	3.94079346151E212	1.271027413889951521423204
251	-9.27402089917E212	1.271027413889951521423411
252	-1.53792247833E215	1.271027413889951521423587
253	4.17365586728E215	1.271027413889951521423739
254	6.09718075121E217	1.271027413889951521423868
255	-1.87702245373E218	1.271027413889951521423980

 

We seem to arrive at a value d( 1, 0.5) ~ 1.27102741388995152142.., which reinserted into that powerseries (and again be Noerlund-summed) gives a reasonable approximation to d(d(1,0.5),0.5) = d(1,1) .

However, it is possible that this is still only a local approximation. It seems, that the growthrate of the terms is even more than hypergeometric; a plot of the quotients of successive coefficients indicates strongly, that in the average the coefficients grow dependent on the index k like O((k!)^1+δ) (with oscillations) where if δ>0 significantly the used Noerlund-summation is not strong enough. The following plot shows the growthrate by the formula

                 

 

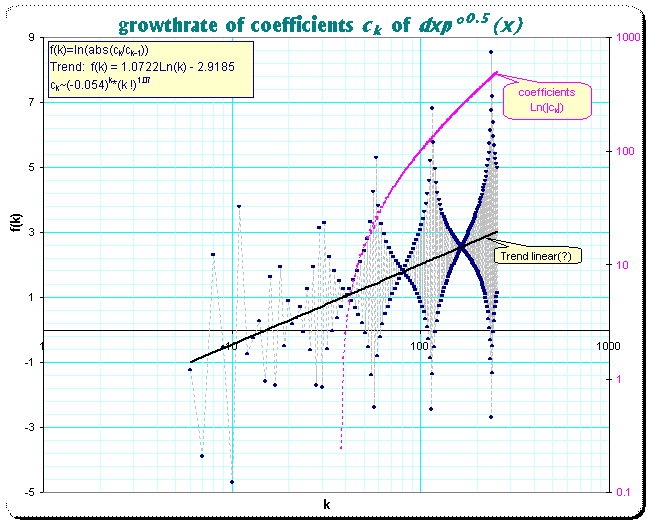
Note: I used dxp(x,h) in the program for the drawing of the graphic instead of d(x,h)

Trend: (estimated using Excel)
                ln(c_k/c_k-1) = 1.0722ln(k)-2.9185
                 c_k ~(-0.054)^k (k!)^1.07 

 

 

Gottfried Helms

(Last update at 12.2.2011 // 3.Nov.2010)

[Comtet]        Comtet, L;
Advanced Combinatorics (1974 edition)
D. Reidel Publishing Company, Dordrecht - Holland

[A&S]             Abramowitz, M. and Stegun, I.A.;
Handbook of mathematical functions 9th printing
page 824; online at http://www.math.sfu.ca/~cbm/aands/

[Erdös]           Erdös, Paul , Jabotinsky, Eri;
On analytic iteration
J. Anal. Math. 8, 361-376 (1961)  (also online at digicenter göttingen)

[Baker]           Baker, I.N.;
Zusammensetzung ganzer Funktionen,
Math Zeitschr. Bd. 69 pp 121-163 (1958)  (also online at digicenter göttingen)

Projectindex

                               http://go.helms-net.de/math
                               http://go.helms-net.de/math/tetdocs