A discussion of the computation of a extremely diverging series.

Keywords: tetration, Iterationseries, series of powertowers, Eulersummation, Shanks-summation, Analytic continuation

Preface: this conversation took place in June 2007 in the newsgroup sci.math.research. For this edition I collected the archived messages from groups.google.com, formatted them and at some places I corrected words and inserted explanative phrases.

Gottfried Helms, Kassel 9'2010

 

 

                1 - exp(1) + exp(exp(1)) - exp(exp(exp(1)))   +  - ... =?

I asked this in sci.math, but without useful success. Perhaps the subject is more appropriate here... I'm considering divergent summation, and wouldn't have a clue, with which technique one would access this problem. Recently I found a possible solution, which however depends on proofs for convergence or at least summability of intermediate result.

For a start,  a current approximation was

                 0.246960868[386...

Here the explanation which I sent to sci.math, inserted comments marked by "**>". Is someone out here, who could comment on the following?

TIA -
Gottfried Helms

(posting to sci.math, answering to a respondent) [editet in some wordings, G.H. 9'2010]

Well, to some divergent series a value can be assigned by Cesaro-,Euler-, or Borel-summation. To others these summation-methods do not suffice to "limit" them in terms of their partial sums. Now this is a very badly diverging series...  It occurs in a certain "experimental" context, where I look at formal powerseries of the iterated exponential. Assume, I have the coefficients of the formal powerseries of x in a vector   V(x) = [1,x,x^2,x^3,...] which I call a "vandermonde-vector". Now assume another vector A1, containing   A1 = [1/0!, 1/1!, 1/2!, ...] then the dotproduct of the rowvector V(x)~ and A1 is just the expression for the powerseries/the symbolic reference and also for the evaluation of exp(x):   V(x)~ * A1 = exp(x) Now I have another vector A2, and this performs  V(x) ~ * A2 = exp(x)^2 and another A0, which simply performs V(x) ~ * A0 = exp(x)^0 = 1  and assume, I have a set of vectors A0, A1, A2, ... collected in a matrix B, giving  V(x)~ * B= [ 1, exp(x), exp(x)^2, exp(x)^3,...] then the result vector is again of the vandermonde-type and noting  V(x) ~ * B = V(exp(x))~ I say, B transforms a powerseries in x in one of exp(x).

Now, if I consider iterated application, then I have  V(x)~           * B = V(exp(x))~  V(exp(x))~      * B = V(exp(exp(x)))~  V(exp(exp(x)))~ * B = V(exp(exp(exp(x))))~  ... and so on. Let me write the iterated exponentiation of a value x using a fixed base b with the number of iterations h (for "iteration-height") x^^h = exp(exp(…(exp(x))…)) with h iterations                          (note: this is a misuse contrary to the common "^^" operator – notation!) Then I can write this in terms of powers of B:  V(x)~           * B^0 = V(x)~      = V(x^^0)~  V(x)~           * B^1 = V(exp(x))~ = V(x^^1)~  V(x)~           * B^2 = V(x^^2)~  V(x)~           * B^3 = V(x^^3)~  ...  V(x)~           * B^k = V(x^^k)~  ... B is not triangular, so its powers are not defined for infinite dimension - but it seems, that comparing the powers of B with increasing finite dimensions, there is a convergence in the sum in the dominating terms. (edit 9'2010: shortly later I found a solution how to express each entry of each power of B with a finite composition of powers of logs and scalars, so this assumtion can now be justified) So assume a reasonable behaviour for the beginning.

The alternating sum of theses values could then be written in terms of a geometric series of B:  V(x)~ * (B^0 -B^1 + B^2 - B^3 + B^4 ...)        = V(x)~ - V(exp(x))~ + V(exp(exp(x))) - ... For a geometric series the shorthand formula is also valid for matrices,    (I - B + B^2 - B^3 + B^4 -+...) * ( I + B) = I    (I - B + B^2 - B^3 + B^4 -+...)            = I * (I + B)^-1 writing M for the reciprocal of the term    M = (I + B)^-1 *if* the powers can be used *and* the parenthese is invertible. Now for finite dimensions d, the matrices M_d seems to stabilize with higher d, and a convergent for M_d with d->oo seems reasonable, so practically I assume the finite version of M_d with d=64 as sufficient precise, where I calculate with float-precision of about 200 digits (Pari/Gp), and final approximations to ~ 12 significant digits for display.

The top-left-submatrix of M_d for d>60 is about:   1/2        -0.24696      -0.036280       0.063037   ....     0         0.60330       -0.38514       -0.12045     0        -0.11631        0.61686       -0.42321     0     -0.00013547       -0.16041        0.59960     0       0.0081171      -0.013595       -0.18060     0     0.000074344       0.014385      -0.021246     0      -0.0012697      0.0031833       0.017801     0     -0.00010936     -0.0023863      0.0059199   .... where the sequences of the absolute values in the columns seem to converge to zero. For the sum of the first column of M I get now   lim   V(1)~ * M[,0]   = 1/2 which is obvious since   V(1)~ * column([1/2,0,0,0,...]) = 1/2 and this is implying, or a shorthand for, the first column (columnindex c=0) of the explicite and divergent rowvectorsum of all V(x)~ * B^k [*,0] : 1 - 1 + 1 - 1 + ...    [1,     x,           x^2,        x^3,    x^4,...] - [1,   exp(x),      exp(x)^2,                 ...] + [1, exp(exp(x)), exp(exp(x))^2 ,             ...] - .... + .... which in the sense of Cesaro or Euler-summation gives 1/2 and trivally equals the dot-product V(x)~* col(1,0,0,0,…) in the matrix-equation . Analoguously I apply this to the second column, M[,1] , which still seems to be convergent with x=1.

lim  V(1)~ * M[,1] = 0.246960868[386... (Again implicitely) this expresses the replacement for the alternating sum     x - exp(x) + exp(exp(x)) - ... of the first columns of all V(x)~ * B^k by its construction. The intention of my question was, -besides of the amazing formulation of the problem - to get crosschecks with different methods, and still would like to see, whether this result is conform with other methods. <**comment for this conversation:>    I *assumed* from heuristics, that M_d stabilizes with higher d and thus in principle we would expect some summability for the alternating sums of V(x)~ * B^k, but I didn't work this out so far. Note, that an equivalent, but somehow inverse idea, can be checked easily by low order summation-techniques:  x - log(1+x) + log(1+log(1+x)) - log(1+log(1+log(1+x))) +... -   ... which has oscillating divergence, which one however can handle by Eulersummation, for instance. Gottfried Helms

 

What does your method give when the base of your iterated exponentiation is changed from e to sqrt(2)?  When the latter base is used the terms are bounded and you will get an Euler-summable expression, whose Euler sum can be compared with what your method gives.

--OL

 

Am 24.06.2007 14:48 schrieb Oscar Lanzi III:

What I get is, even with (my) Eulersum of order 1 (direct summing)

dim = 64
%pri B =    1.0*dFac(-1)*PInv*St2F * P~   \\ the initial version of B, performing summing with parameter exp(1)
%pri B_test = dV(log(2)/2) * B           \\ test-variant which performs with parameter sqrt(2)

1) Check appropriateness of B_test

----------------------------------------------------

First power of matrix/first iteration

%pri ESum(1.0)*dV(1)*B_test              \\ example-summation , Eulersum of low order 1 is possible
==>  1.00000   1.41421   2.00000   2.82843   4.00000   5.65685   8.00000  (…)

The row above means: using b=sqrt(2)

    [1,1,1,1...]  ==> [1, b,  b^2 , b^3, ...]

---

Second power of matrix/second iteration

%pri ESum(1.0)*dV(1) * B_test^2         \\ example-summation , Eulersum of low order 1 is possible
 ==> 1.00000   1.63253   2.66514   4.35092   7.10299   11.5958   18.9305  (…)

This means:

   [1,1,1,1...]  ==> [1, b^b,  (b^b)^2 , (b^b)^3, ...]

---

Third power of matrix/third iteration

%pri ESum(1.0)*dV(1) * B_test^3
==> [ 1.00000   1.76084   3.10056   5.45958   9.61345   16.9277   29.8070   (…)]

This means:

    [1,1,1,1...]  ==> [1, b^b^b,  (b^b^b)^2 , (b^b^b)^3, ...]

----------------------------------------------------

 

2) Now check results of infinitely iterated use of B_test by use of M_test

----------------------------------------------------

B1_test = matid(n) + B_test ;

                compute the inverse of B1 by inversion of its L,D,U-components

tmp = CV_LR(B1_test);                      \\ compute L-D-U - components of tst
                                           \\ result in matrices CV_L  CV_D  CV_R

dim = 64   \\ compute the Inverse of I + B_test using different dimensions

M_test = EMMul(VE(CV_RInv,dim),  VE(CV_DInv*CV_LInv,dim), 1.0)
              \\ compute the inverse matrix M_test of B1_test by L-D-U-components
              \\ with    dim as selectable dimension,
              \\         implicte euler-summation (here order 1.0)
              \\         in the matrix-multiplications

\\ results
%pri ESum(1.0)*dV(1)*M_test                   \\ Eulersum(1.0)

==>  [0.500000    0.362302    0.201330    0.0223437   -0.161780   (…) ]

 

where in the second column is the interesting result.

Note, that for summation of the more right columns higher orders of the Euler-summation may be needed, so these numbers need be crosschecked (but are uninteresting in our current context, anyway.)

---------------------------------------------------------

 

The result of the above operations is now:

 

 x= lim  1 - sqrt(2)^1 + sqrt(2)^sqrt(2)^1 - sqrt(2)^sqrt(2)^sqrt(2)^1 + ... - ...
  = lim  1- b + b^^2 – b^^3 + b^^4 - … + …
 x ~  0.3623015472668659

 

Curious, whether this result makes sense...

 

Note, that using V(2) as initial powerseries we get the expected

%pri ESum(1.0)*dV(2)*M_test                   \\ Eulersum(1.0)

==> [ 0.500000   1.00000   2.00000   4.00000   8.00000   16.0000   32.0000  (…) ]

and in the second column we have the implicte computation of:

 x= lim  2 - sqrt(2)^2 + sqrt(2)^sqrt(2)^2 - sqrt(2)^sqrt(2)^sqrt(2)^2 + ... - ...
  = 1.000

 

Gottfried Helms

Am 24.06.2007 14:48 schrieb Oscar Lanzi III:

Well, what I get by direct Eulersummation is

 y = lim sqrt(2) - sqrt(2)^sqrt(2) + ...  \\ Eulersummation

then

 y ~ 0.6376984527331341...

Let x be my previous result

 x ~  0.3623015472668659...

then we have

  y = 1.0000000000... - x

I think I should look for a small correction... Thanks for the hint concerning sqrt(2).

Gottfried Helms

Am 24.06.2007 14:48 schrieb Oscar Lanzi III:

Correction of my previous post:

I had a different series, so both results are perfectly compatible:

I had (citing myself here):

and by direct summation I was missing the first term 1:

and indeed

                   x = 1 - y

So this seems to be a one-example confirmation of my method.

Gottfried

Good.

Now test this thing by approaching and then breaking through the singularity (with respect to the boundedness of the terms and thus Euler summation) at b(ase) = exp(1/e) = 1.444+.  I would recommend proceeding in two stages: first examine the behavior as you come up to the Euler-summation singularity; then, if that is satisfactory, step beyond it with your method.

 

Part 1:  The approach

We have seen what the sum (both Euler's and yours) is at b = sqrt(2) = 1.414+.  Examine the Euler sum for b = 1.43, 1.44, 1.444.  You can also try your method if you wish for these bases, although the result for b = sqrt(2) seems to indicate that you'll just get back the Euler sum.

What you need to see is evidence that the Euler sum does _not_ duplicate the square root singularity with b that we get in the individual terms. To wit, as b approaches e^(1/e) from below the n-th term apporaches a*((-1)^(n-1)) with a defined by b = a^(1/a) and a <= e.  This asymptotic behavior contributes a/2 to the Euler sum, where a and therefore a/2 will contain a square-root singularity.  The deviations of the terms from this behavior for finite n must be such as to cancel out this square root singularity. 

*If they don't, then an analytic continuation across b = e^(1/e) will surely go into complex numbers, turning your real sums into sauce*. 

To check this, plot your sums against a (or against sqrt[(exp(1/e)-b]) and against b, and see which relation appears (essentially) linear.  What you want, of course, is linear behavior versus b.  This method is not foolproof, but it will at least screen out the most obvious possible pitfall in your scheme.

 

Part 2:  Over the edge

If Part 1 appears satisfactory, examine the sum by your method (Euler's will no longer work) for b = 1.45, 1.46, 1.47.  Compare these results with the earlier ones for b = 1.43-1.444, to see if there is reasonably smooth behavior.  If yes, you have an apparently suitable analytic continuation that can be applied for "large" values of b such as e.

Have fun!  :-)

--OL

 

Am 25.06.2007 13:27 schrieb Oscar Lanzi III:

:-) Just came across it. How did you get the idea, that this point would produce a singularity, btw?

Also I used different notation for indication of the base. The indicated bases would be           
                1/e = 0.3678794411714423... in my notation below.
(For exp(1/e) in my notation I get  ~ 0.3562483198426627...)

Well, I'll try to configure my testenvironment according to this...

Here I have some results; I'll see, whether I can go more into detail tomorrow to examine it in the near of s = 1/e +- eps and to do some plots. (I'm using "s" in the following to prevent confusion with your notation of "b")

I checked the intermediate summation-terms of the matrix- multiplication for apparent divergence. The following entries seem to be good approximations without need of high orders of Eulersummation:

1 - 5  + 5^5   - 5^5^5    +  ... %445 = 0.1976203324895644
1 - pi + pi^pi - pi^pi^pi +  ... %432 = 0.2324670739643584
1 - e  + e^e   - e^e^e    +  ... %457 = 0.2469608978527557
1 - 2  + 2^2   - 2^2^2    +  ... %469 = 0.2874086990716591

s = phi+1 (= 1.6180339887498948..)
1 - s  + s^s   - s^s^s    +  ... %507 = 0.3278048495149163

s=sqrt(2)
1 - s  + s^s   - s^s^s    +  ... %481 = 0.3623015472668659

s = phi (= 0.6180339887498948..)
1 - s  + s^s   - s^s^s    +  ... %494 = 0.7861534997409138

s = 1/2
1 - s  + s^s   - s^s^s    +  ... %519 = 0.9382530028218765

\\ the following are questionable --------------
\\    1/e ~ 0.3678794411714423

s = 1/e + 0.01
1 - s  + s^s   - s^s^s    + ...  %531 = 1.172056144413609

s = 1/e
1 - s  + s^s   - s^s^s    + ... --- division by zero ---

s = 1/e-0.01
1 - s  + s^s   - s^s^s    + ..  %551 = 1.223179007248831

s = 0.01
1 - s  + s^s   - s^s^s    + ..  --- seems to diverge ---

\\ the following is specifically questionable, since my Euler-sum
\\ procedure is not configured well for complex summation,
\\ although the summation-terms diverge "not too strong"
\\
\\ the implicite value log(-1/2) is used by the Pari-convention as
\\ ~  -0.6931471805599453 + 3.141592653589793*I

s = -1/2
1 - s  + s^s   - s^s^s    + ..  %592 = 0.3755075014152616 - 1.118700997443251*I

Next I'll try your suggestion to get more results near the singularity and speed up the computation to get sufficient coordinates for a plot.

Thanks for the comment!

Gottfried

I just saw your result for low bases.  There you run into a singularity not only with respect to Euler summation, but with respect to the actual sum obtained by any method.

The singularity for s < 1 occurs at s = exp(-e), not at s = 1/e.  The quantity that's 1/e at this point is the limit of the absolute values of the terms; to wit, given s = exp(-e), the sequence 1, s, s^s, etc. converges to 1/e.  Above this, up to s = exp(1/e), the Euler sums converge; and as we have seen, for still larger s we can achieve convergence with nonlinear methods (both the iterated Shanks trnasformation and yours).  But at s = exp(-e) the Euler sum becomes divergent.  The divergent behavior is understood by decomposing rendering the summation terms as

                a*(-1)n-1 + dn

where a is the limiting absolute values of the terms as described preciously.  The deviations dn asymptotically satisfy dn+1/dn = –ln a, so the boundaries of convergence are given by a = e and a = 1/e.  For the former case (s = exp(1/e)) the signs of the dn terms altternate, which enables convergence simply because the absolute values of the dn slowly die out.  But for s < 1 the signs of the dn terms are all positive, and at s = exp(-e) where the limiting term ratio hits 1, they go to zero too slowly for convergence.

Below s = exp(-e) the sequence 1, s, s^s, etc. does not blow up.  It bifurcates; as s --> 0+ the terms alternately approach 1 and 0.  In your alternating series this produces a positive bias; the series diverges linearly.  Such a linear diovergence cannot be removed with standard summation methods, so I am not surprised to see that your method likewise breaks down at s = 0.01 (which is less than 1/e).  

What is the nature of the singularity at s = exp(-e)?  Given the behavior of the dn above we would expect a first-order pole.  But a function should be continuable across (or around) a pole.  There must be some hidden structure that prevents such contiunuation.   Curiouser and curiouser ... .

Thanks for getting back to me.

--OL

 

I just added a documentation about the terms for the Euler-summation on the real axis near the singularity.  It looks very good and is at

                 http://go.helms-net.de/math/binomial_new/PowertowerproblemDocSummatio...

Gottfried

----
Gottfried Helms, Kassel

 

The "singularity" I was referring to has to do with the terms of the series that suddenly go from bounded to increasing extremely fast. Therefore there is a catastrophic breakdown of the Euler summation.

But it turns out that the iterated Shanks extrapolation continues to converge, and that its results indicate continuous behavior across the Euler-summation singularity.  Following are sums I obtained using Microsoft Excel:

Base                       Sum
1.43                        0.359117
1.44                        0.357152
-------Euler-summation Singularity--------
1.45                        0.355226
1.46                        0.353346*
1.47                        0.351477*

                               * Slight uncertainty since I could get only a few partial sums before the terms overflowed.

The implication is that sums are definable across the Euler-summation sigularity; that is, the singularity is removable.  But for bases substantially larger than e^(1/e) in my notation, the Shanks mthod becomes computationally unfeasible and we would have to rely on your method.

--OL

 

Am 26.06.2007 03:52 schrieb Oscar Lanzi III:

Hmm - I'm still not prepared to comment on this precisely.

However, considering an email which I got today urged me, to try to differentiate two things, whose mixture may be a source of misconception and may confuse (at least my) part of discussion.  It appears now to me, that we possibly discuss two essential different things here, which surely cover overlapping aspects. I'm discussing an infinite sum of finite entities - each term in the sum is finite. The other side is the infinite powertower itself. This construct does not occur in the given sum - however attracted and partly dominated unconsciously my attention and focus over the last days.

Surely the bounds, given for the infinite powertower are relevant for the mentioned sum and may or may not exactly establish bounds for the base-parameter of the given infinite sum. It reminds me to the difference between formulating a lemma for the geometric series: an infinite sum of finite entities (powers of a certain parameter) and for the infinite power of a parameter itself.

Well - for the infinite power there is no expression, so let's assume an infinite one-parameter continued fraction, for which a limiting value can be found but which would be essentially different from an infinite sum of rational continued fractions.

Another analogy may be given by the zeta-series. For each real parameter >1 it is conventionally convergent, and for each real parameter <=1 it is divergent.  But also here we deal with an infinite sum of finite entities, in contrast to a power of an infinite entity itself.

 

So I feel, this aspect should be considered more explicitely...

 

With the "alternating sum of increasing powertowers"  of a certain base I think now, the best formulation  is, that my process gives coefficents ak for a  polynomial, which then replaces the term-by-term  summation of the reflected powertower-series  and also expands the domain for the base-parameter,  which are defined by the bounds for the base-parameter  for an individual infinite powertower.

Also the coefficients a_k are parameterspecific, where the parameter s is the base.

The variable x in the polynomial with coefficients ak, (which are dependend on s), allows the computation of

                 S(s,x) =  x - s^x + s^s^x - s^s^s^x + ... -

in terms of a polynomial in x instead. The x at the top of  the powertowers are an aspect of parametrizing such a sum  different from what we discussed before (and this may  also be of less interest - we had simply set it to 1 in our  discussion).

It is comparable -for another instance- with the Stieltjes-  constants as coefficients a_k of a polynomial in x, which  allow then to compute the zeta-series zeta(x) in terms of  a polynomial.

I'm not sure, how far I got this right and formulated well,  I appreciate comments on this, too.

Gottfried

----
Gottfried Helms, Kassel

 

Oscar -

putting some aspects of your previous posts together.

The best presentation of my method is to say that it provides for

     S(s,x) = x - s^x + s^s^x - s^s^s^x + ... -                           (*1a)

here for x=1

     S(s):= S(s,1) = 1 - s + s^s - s^s^s + ... -                          (*1b)

a polynomial/powerseries representation in terms of coefficients as_k depending on s

     S(s,x) =  as_0 +  as_1 x + as_2 x^2 + as_3 x^3 + ...                 (*2a)
     S(s,1) =  as_0 +  as_1   + as_2     + as_3     + ...                 (*2b)
     S(s,0) =  as_0                                                       (*2c)

For the documentation of the behaviour of S(s) in my method, I make use of  the following identity.

It is according to (*1a) and (*1b)

     S(s,1) = 1 - s^1 + s^s^1 - s^s^s^1 + ... -
     S(s,0) = 0 -  1 +   s^1  -  s^s^1  +  s^s^s^1 + ... -

  from where in the limit it should be

     S(s,1) = - S(s,0)                                                     (*3)

By (*2b) and (*2c) it is

     S(s,1) =  as_0 +  as_1   + as_2 + as_3 + ...
     S(s,0) =  as_0

and since by (*3)  S(s,1) = - S(s,0) we have, that S(s,1) is completely explained by the first of the coefficients as_0 and thus

     S(s)  = - as_0

Now as_0 is itself the result of a vector-product, and to check its behaviour I document its individual additive components

     as_0 = bs_0 + bs_1 + bs_2 + ...

so that the best simplificated result of my method is then (assuming x=1)

     S(s) =  - (  bs_0 + bs_1  + bs_2  + bs_3  + ... )                      (*4)

Let T(s) denote the infinite powertower s^s^s^s^s... .

For s providing the convergent cases T(s) I crosschecked my method (*4) for computing S(s) by usual Eulersummation of the terms (*1b), where I got identity in terms of float-arithmetic approximation.

That means all s in  e^-e +eps < s < e^(1/e), where eps ~ 2^-12; this includes also s=sqrt(2).

For the coefficients bs_k in (*4) I get nicely decreasing absolute values of alternating signs, where however the alternating behaviour is not strict.

A small table for various s

param  !   coefficients                                          sum(- bs_k)
s      !   bs_0   bs_1     bs_2     bs_3    bs_4   ...             S(s)
-------+---------------------------------------------------------------------
1      !   0      -0.5      0       0       0    ...               1/2
1.0625 !   0      -0.47    0.00076  1e-6    2e-8   ...             0.4706
1.4375 !   0      -0.367   0.009   -6e-6    1e-5   .(decreasing)   0.3576
1.5    !   0      -0.356   0.010   -1e-4    5e-5   .(decreasing)   0.3461
3      !   0      -0.238  -0.002   -2e-4    6e-4   .(decreasing)   0.2368
7      !   0      -0.170  -0.017    4e-3    2e-3   .(decreasing)   0.1795
e^2    !   0      -0.167  -0.018    4e-3    2e-3                   0.1769
e^3    !   0      -0.125  -0.023    2e-4    3e-3                   0.1421

where for higher s the dominant term is further decreasing in absolute value and with a vague floating the subsequent terms are still decreasing, while the rate of decrease seems to diminuish. But this may be due to the finite dimension of my matrices and I'll check this later.

For s = exp(k) I seem to get nice approximations to rationals for bs_1, saying

     bs_1 = -1/2 * 1/(k+1)

which explains then the method-internal singularity at s = exp(-1).

With decreasing s I get less bs_k which are negative, so the alternating character disppears and at s = e^(-e) I get a series with only positive terms, which also increase, and thus cannot be summed to a finite value.

param  !   coefficients                                          sum(- bs_k)
s      !   bs_0   bs_1     bs_2     bs_3    bs_4   ...             S(s)
-------+---------------------------------------------------------------------
e^(-e) !   0      0.291    1.332    2.369   3.210                 -inf-

 

I couldn't reproduce that behave of your version of the Euler-summation.

The terms to be summed are for the method (*1b), s= sqrt(2)  (correction from a later post included, G.H.)

  1, -1.4142136, 1.6325269, -1.7608396, 1.8409109, -1.8927127, 1.9269997, ...

If I apply my implementation of Euler-summation I get the following smooth sequence of partial sums:

  0.50000000   0.39644661   0.37195908   0.36534037   0.36333599   0.36267423

which stabilizes at about the 20'th term in the last displayed digit to   0.36230155

Here I don't know, what's going on compared to your report?

<this table was inserted by me 09'2010>

1.43        0.359116949394
1.44        0.357152020439
1.45        0.355226327435
1.46        0.353338749529
1.47        0.351488199418

                all computations without overflow and stable digits up to ca 20'th dec position

Regards -
Gottfried

---
Gottfried Helms, Kassel

Based on the numerical values from your table it ap[pears that the Shanks and Helms methods agree across s = exp(1/e) as was originally demanded.  Thus the Helms method appears to be valid for the original problem with s = e.

We seem to agree that s = exp(-e) represents a "true" singularity where convergence breaks down.  Numerical investigation of the sums as s --> exp(-e)+ indicates not a pole as I had first conjectured, but a branch point; if s = exp(-e)+t then the sum grows in proportion to t^(-1/2) (try it!).  This accounts for the lack of analytic continuability.  In the other direction your bs_0 values point to an asymptotic approach to 1/(2*ln s+2) for large s.  Already for s = e we are rather close to this limit.

--OL

 

Am 30.06.2007 15:45 schrieb Oscar Lanzi III:

Very good! I'll study these informations to add them to the article.

So it seems, that this method has a resonable degree of verification, to consider its emission to the "scientific knowledgebase".

How to proceed?

a)        I feel not competent to prove the appropriateness of equivalence of the sum of powers of B and the inversion of (I+B). If this is indeed needed (what    I assume) then proving the general summability of B^0 - B^1 + B^2... must be done in terms of growthrate- analyses for the entries of such a sum of matrices, and already for the individual powers of B and its parametrized versions(*1).

Although I've read the books of G.H.Hardy and K.Knopp about infinite, divergent series, I feel not to be experienced enough to apply the required limiting criteria here to a sufficient extent. Here I needed help, or I have to leave that whole part open for further survey.

b)       I don't have a clue about the requirements for submitting articles, and even about journals, which     may be interested in that subject. Also here I needed hints and advice.

c)        ???

Regards -

Gottfried

 

 

*)        For the interesting second column of B^2 I found  it consisting of Bell-numbers with inverse factorial  scaling, which is meaningful, since I know that  the Bell-numbers define the powerseries in x for  the computation of exp(exp(x)).

 Since these Bell-numbers can also be computed by  exponentiaton of the pascal matrix P, this indicates,  that iterated exponentiation of P (which is itself  the first iterate of such an exponentiation then)  may describe the behave of this critical column in  the powers of B as well.

----

Gottfried Helms, Kassel

 

Am 01.07.2007 13:05 schrieb Gottfried Helms:

I seem to have a solution for this problem. The  entries of powers of B (as well as of the parametrized  version) can, though B itself is a non-triangular-matrix  of infinite size, apparently be described by exponentials  of nilpotent triangular pascal-matrices (P - I), so  they seem to be provable of finite size. If that holds,  then one can say that they all are expressible as  finite combinations of logarithms and exponentials,  and the equivalence of M and the alternating sum of  powers of B and Bs can (principally) be settled.

Gottfried

----
Gottfried Helms, Kassel

 

I compiled an overview about my summing-method in

                  http://go.helms-net.de/math/binomial_new/10_4_Powertower.pdf

where the method is explained in more detail, and is reflected regarding the discussion I had with Oscar Lanzi III .

Also I rewrote the study of the singularity point in

  http://go.helms-net.de/math/binomial_new/PowertowerproblemDocSummatio...

------

@ Oscar :

Oscar –

thanks again for your comments, they are helpful to make me review open questions in my approach. Meanwhile I searched for material about tetration and get additional caveats concerning the range of validity of the method. I'll answer to your recent letters in more detail tomorrow, I'm having doubts about the validity of Euler-summation at and beyond the critical point exp(-1), which you mentioned.

Gottfried

-------
Gottfried Helms, Kassel

 

Am 24.06.2007 00:03 schrieb Gottfried Helms:

I can add some more information about the matrix B1 = (I + B) and M = B1^-1 which support the assumption of stabilizing of M and convergence/ summability of the column-sums of M according to   V(1)~ * M

---------------------------------------------------------

To invert B1 I decompose it into L,D,U - components, where L is a lower left triangular matrix, D is diagonal, U is an upper right triangular matrix.

With increasing dimension d the coefficents in L,D,U are constant, only new rows/columns are added.

Here I give the images for d = 12, where for display I reduce the rows to 8 and columns to 6

The left component L:
VE(tL,8,6):
  1         .           .         .            .                 .
  0         1           .         .            .                 .
  0       1/4           1         .            .                 .
  0      1/12        7/15         1            .                 .
  0      1/48         1/4     19/28            1                 .
  0     1/240      31/300     13/28      103/115                 1
  0    1/1440       7/200   211/840    5774/7935       51775/46483
  0   1/10080   127/12600    19/168   7499/15870   2028343/1952286

-----------------------------------------------

in float display:

1.0*VE(tL,8,6):
  1.00000              .           .          .          .         .
        0        1.00000           .          .          .         .
        0       0.250000     1.00000          .          .         .
        0      0.0833333    0.466667    1.00000          .         .
        0      0.0208333    0.250000   0.678571    1.00000         .
        0     0.00416667    0.103333   0.464286   0.895652   1.00000
        0    0.000694444   0.0350000   0.251190   0.727662   1.11385
        0   0.0000992063   0.0100794   0.113095   0.472527   1.03896

=======================================================================

The right component R is:

VE(tR,8,6):
  1   1/2   1/2   1/2       1/2         1/2
  .     1     1   3/2         2         5/2
  .     .     1   3/2      14/5         9/2
  .     .     .     1   212/105        13/3
  .     .     .     .         1   2695/1058
  .     .     .     .         .           1
  .     .     .     .         .           0
  .     .     .     .         .           0

-----------------------------------------------

in float display:

1.0*VE(tR,8,6):
   1.00000   0.500000   0.500000   0.500000   0.500000   0.500000
        .    1.00000    1.00000    1.50000    2.00000    2.50000
        .          .    1.00000    1.50000    2.80000    4.50000
        .          .          .    1.00000    2.01905    4.33333
        .          .          .          .    1.00000    2.54726
        .          .          .          .          .    1.00000
        .          .          .          .          .          0
        .          .          .          .          .          0

==============================================================

The diagonal is

VE(tD,8):
  2   2   5/2   7/2   529/105   2021/276   497335/46483   77937481/4973350

1.0*VE(tD,8):
  2.00000   2.00000   2.50000   3.50000   5.03810   7.32246   10.6993   15.6710

Note, that the entries of this diagonal do not change regardless of the dimension; increasing the dimension simply adds new values.

=======================================================================

Now, to invert B1 means to use the inverse of the three components, where because of their triangularity plus the consistency of coefficients regarding the size of dimension the coefficients are again consistent:

The inverse of the diagonal D in rational and float display

1.0*tDinv,tDinv:
                                                  1/2    0.500000
                                                  1/2    0.500000
                                                  2/5    0.400000
                                                  2/7    0.285714
                                              105/529    0.198488
                                             276/2021    0.136566
                                         46483/497335   0.0934642
                                     4973350/77937481   0.0638120
                           245503065150/5644742532671   0.0434923
                 18966334909774560/640455736601965177   0.0296138
        322789691247390449208/16020371227049741794583   0.0201487
  212540844137878775546487/15511826733078660216267418   0.0137019

-----------------------------------------------

The inverse of the right component R

VE(tRInv,8,8):
  1   -1/2    0    1/4     -1/210   -2039/6348     2831/92966      2597513/4774416
  .      1   -1      0        4/5      -20/529   -55230/46483         70259/397868
  .      .    1   -3/2       8/35      750/529   -20610/46483       -899619/397868
  .      .    .      1   -212/105    1285/1587    90492/46483      -1496523/994670
  .      .    .      .          1   -2695/1058    78864/46483      4426723/1989340
  .      .    .      .          .            1     -6210/2021      5714667/1989340
  .      .    .      .          .            .              1   -42932869/11936040
  .      .    .      .          .            .              .                    1

1.0*VE(tRInv,8,8):
  1.00000   -0.500000          0   0.250000   -0.00476190    -0.321204   0.0304520   0.544048
        .     1.00000   -1.00000          0      0.800000   -0.0378072    -1.18818   0.176589
        .           .    1.00000   -1.50000      0.228571      1.41777   -0.443388   -2.26110
        .           .          .    1.00000      -2.01905     0.809704     1.94678   -1.50454
        .           .          .          .       1.00000     -2.54726     1.69662    2.22522
        .           .          .          .             .      1.00000    -3.07274    2.87264
        .           .          .          .             .            .     1.00000   -3.59691
        .           .          .          .             .            .           .    1.00000

-----------------------------------------------

Inverse of the left-component

VE(tLInv,8,8):
  1                .                  .                   .                    .                 .                  .   .
  0                1                  .                   .                    .                 .                  .   .
  0             -1/4                  1                   .                    .                 .                  .   .
  0             1/30              -7/15                   1                    .                 .                  .   .
  0            2/105               1/15              -19/28                    1                 .                  .   .
  0            -1/92             37/690              33/230             -103/115                 1                  .   .
  0      -385/185932       -3628/139449      153891/1859320        188227/697245      -51775/46483                  1   .
  0   38677/10444035   -513748/52220175   -4511833/87033625   25638092/261100875   1861897/4177614   -3314476/2486675   1

1.0*VE(tLInv,8,8):
  1.00000             .             .            .           .          .          .         .
        0       1.00000             .            .           .          .          .         .
        0     -0.250000       1.00000            .           .          .          .         .
        0     0.0333333     -0.466667      1.00000           .          .          .         .
        0     0.0190476     0.0666667    -0.678571     1.00000          .          .         .
        0    -0.0108696     0.0536232     0.143478   -0.895652    1.00000          .         .
        0   -0.00207065    -0.0260167    0.0827674    0.269958   -1.11385    1.00000         .
        0    0.00370326   -0.00983811   -0.0518401   0.0981923   0.445684   -1.33289   1.00000

=======================================================================

Now M_d for a certain dimension d is

         M_d = B1_d^-1  =  R_d^-1 * D_d^-1 * L_d^-1

and one had to show, that the occuring partial sums for the entries of M_d,  for d = 1 to inf are either convergent or can be limited by a summation technique.

For this analytical expressions for the entries in R^-1, D^-1,L^-1 are required which I don't see at the moment. But since the entries have alternating signs, and the values in the inverted diagonal seem to decrease, I think, asymptotics should be sufficient for a first estimate of the validity of the general idea and the given provisorial result.

Gottfried Helms

[Addition 9'2010]

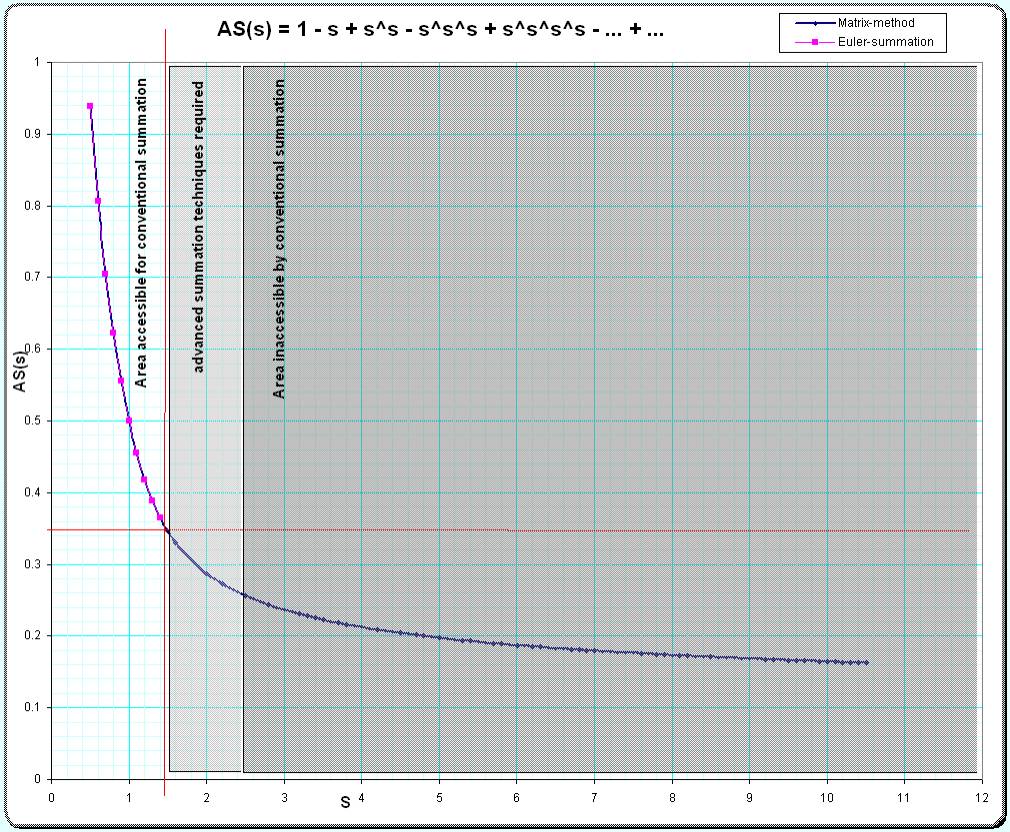
In the picture below I compare the results gotten by the matrix-method (long blue line) and by the Euler- resp. Shanksmethod (short magenta line). The lines are perfectly overlaid in the small-s-region so the dots may indicate the position of the magenta line.

 

 

 

Gottfried Helms, 9'2010