Polynomial regression in a matrix-notation
A self-study attempt using partial derivatives
Regression with a polynomial model
The general problem of a least-squares-approximation/regression
![]()
can be stated as a polynomial version for instance with a polynomial of order 2, where the prognosed yk are estimated based on a quadratic formula on xk :
![]()
where we are searching for the "best" values for a, b, and c, such that -as usual- the sum-of-squares of the residuals is minimal.
The matrix-formulation of the problem
A matrix-expression for the data might look like the following

where we have n data-points and yk and xk are measured, and the rk are the residuals.
Let K denote the vector of sought coefficients K=[a,b,c] and an extension K1=[-1,a,b,c], V the matrix of combined Y and X-data, R the vector of residuals after predicting Y from X so that we have (using ' for transposition)
K1 * V = R
where we want
R * R' = min! //"least-squares"-criterion
So also
K1 * V * V' * K1' = min!
The inner product, divided by the scalar n is just a covariance-matrix which contains the means-of-coproducts indicated by the indexes:
Cov
= V * V' /n = 
Now let the vector of coefficients K1 be used as diagonal and the summing of the matrix-elements indicated by a sum-operation, then, writing
T = dK1 * Cov * dK1'
the matrix T is now
T
= 
and we search a,b,c such that
sum(T) = min
Partial derivatives
We look at it with respect to a, then a must be such that the sum is zero:
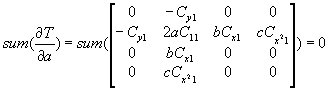
The second derivative is 2C11 which is positive, so in the first direction the extremum at a is a minimum.
The same with respect to b, then also b must be such that the according sum is zero:

The second derivative is 2Cx2 which is positive, so in the second direction the extremum at b is a minimum.
Finally the same with respect to c, then also c must be such that the according sum is zero:

The second derivative is 2Cx4 which is positive, so in the third direction the extremum at c is a minimum.
Result:
In all, if a,b,c are determined in a simultaneous solution, we shall have a minimum in all directions of the function.
Solution
Due to the symmetry of the matrix each of these sums involving partial derivatives gives a very simple equation. We get a system of three equations:

and the solution K by solving
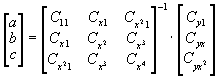
Simplification = linear regression with one independent variable
If that model is reduced to y being a linear function of x then the ansatz is like
ŷ = a + b x
Ŷ = K * X
R = Y – Ŷ
R * R' = min !
where the rowvector K contains the coefficients [a, b ]
Then we get the solution for K by solving

It is interesting, that the usual formula for the regression parameters are immediately visible when we consider, that the x- and y-data are centered; then the means Cy1 and Cx1 are zero and we get the simpler system

which is then the "direct" formula for the simple linear regression.
Generalization = multiple regression
The pattern in the matrixform of the result suggests also that it can easily be generalized to polynomials of higher order; in general, if X denotes the matrix of the x-values and all x^0 to x^m of the m+1 required powers. So we formulate the model with the unknown parameters to be estimated:
ŷ
= b0 + b1 x + b2 x2 + … + bm xm
Ŷ = B * X
R = Y – Ŷ
R * R' = min !
where the rowvector B contains the coefficients [b0, b1, b2, …, bm]
The datamatrix of X has now 1+m rows:
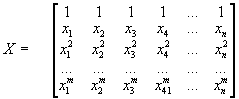
and Y the matrix of y-values looks –as before– like
![]()
then again
COVxx
= X * X ' / n
COVxy = X * Y' /
n
and
![]()
which is also the common formula for the multiple linear regression.
An alternate formulation
Let's look at the matrix T again:
T
= 
We observe, that this is the Hadamard-product
T = Cov # (K1' * K1)
and the derivative wrt a,b,c is the sum of the partial derivatives:
T' = Cov # ( (K1~ * K1) +
![]()
where the sum in each summand separately must equal zero. Exploiting the symmetry we can write
![]()
T
= 
Example:
Dataset; the "empirical" yk were generated using the coefficients a=1, b=3, c=-2 and a uniform random-disturbance "rnd"
|
k |
x |
y |
|
^yk= |
rnd*1000 |
|
1 |
1.00 |
2.01 |
|
2.00 |
14.11 |
|
2 |
2.00 |
-0.99 |
|
-1.00 |
14.35 |
|
3 |
3.00 |
-7.95 |
|
-8.00 |
50.08 |
|
4 |
4.00 |
-19.00 |
|
-19.00 |
2.17 |
|
5 |
5.00 |
-33.94 |
|
-34.00 |
59.29 |
|
6 |
6.00 |
-53.00 |
|
-53.00 |
0.96 |
|
7 |
7.00 |
-75.92 |
|
-76.00 |
77.45 |
|
8 |
8.00 |
-102.93 |
|
-103.00 |
65.07 |
|
9 |
9.00 |
-133.92 |
|
-134.00 |
77.05 |
|
10 |
10.00 |
-168.93 |
|
-169.00 |
70.81 |
|
11 |
11.00 |
-207.94 |
|
-208.00 |
55.75 |
|
12 |
12.00 |
-250.98 |
|
-251.00 |
20.60 |
|
13 |
13.00 |
-297.93 |
|
-298.00 |
68.11 |
|
14 |
14.00 |
-348.94 |
|
-349.00 |
59.29 |
|
15 |
15.00 |
-403.90 |
|
-404.00 |
95.55 |
|
16 |
16.00 |
-462.94 |
|
-463.00 |
64.41 |
|
17 |
17.00 |
-525.90 |
|
-526.00 |
99.84 |
|
18 |
18.00 |
-592.98 |
|
-593.00 |
24.38 |
|
19 |
19.00 |
-663.93 |
|
-664.00 |
67.62 |
|
20 |
20.00 |
-738.97 |
|
-739.00 |
29.57 |
The disturbance (sum-of-squares) of the original vector rnd is
ssqr(rnd)~ 0.06859 .
The procedure gave the matrix COV as
|
|
y |
1 |
x |
x² |
|
y |
118824.98 |
-254.45 |
-3968.40 |
-65499.74 |
|
1 |
-254.45 |
1.00 |
10.50 |
143.50 |
|
x |
-3968.40 |
10.50 |
143.50 |
2205.00 |
|
x² |
-65499.74 |
143.50 |
2205.00 |
36133.30 |
CC is
|
|
1 |
x |
x² |
|
1 |
1.00 |
10.50 |
143.50 |
|
x |
10.50 |
143.50 |
2205.00 |
|
x² |
143.50 |
2205.00 |
36133.30 |
CC-1is
|
|
|
|
|
|
|
11.07 |
-2.16 |
0.09 |
|
|
-2.16 |
0.53 |
-0.02 |
|
|
0.09 |
-0.02 |
0.00 |
The solution K=[a,b,c] is found as [0.9989, 3.0104, -2.0004] .
That solution leads to a improved/smaller ssqr of the residuals:
ssqr(res) ~ 0.01143
This should then be the least possible residual disturbance.