Betrachtungen über eine Faktoranalyse
auf den SGIPT-Seiten zur statistischen Methodik

 

Quelle: Siehe http://www.sgipt.org/wisms/fa/Quader/q02.htm (1)

 

Verwendeter Datensatz: Siehe unten.

 

Motivation und Kontext

Dieses Posting meinerseits in der Mathematik-Newsgruppe beschreibt den Auslöser für meine besondere Aufmerksamkeit, da der Autor der Seite dort eine PCA auf der Basis von Interaktions-Termen diskutiert um damit die Akkuratheit der Reproduktion einer Korrelationsmatrix durch (eine geringe Zahl von) Hauptkomponenten (hier: 3 von 8) zu illustrieren - ein für mich überraschendes Herangehen...

 

 

Posting in news://de.sci.mathematik und news://de.sci.psychologie 30.10.2014:

 

 

 

 

Ich habe mich mal wieder auf den Faktoranalyse-Seiten von Rudolf (SGIPT: http://www.sgipt.org ) umgesehen und dort in

 

 http://www.sgipt.org/wisms/fa/Quader/q00.htm

 

ein merkwürdiges Beispiel gefunden, mit dem die Qualität der Reproduktion einer Korrelationsmatrix via Faktoranalyse nach Hinzufügen eines gewissen Maßes an Fehlerrauschen illustriert werden soll.

 

Es wird hier ein Beispiel verwendet, in dem auf der Basis von 3 "unabhängigen" Zufallsgrößen (also den impliziten und aufzudeckenden Faktoren) 5 abhängige Größen berechnet worden sind, aus deren Korrelationsmatrix (in einer echten) Faktoranalyse dann also die unabhängigen Faktoren wieder identifiziert/sichtbar gemacht werden sollen.

In diesem Beispiel geht es nun zwar lediglich darum, ein Gefühl dafür zu bekommen, wie gut die Korrelationen reproduziert werden, wenn ich nach der Faktoranalyse (genauer genommen PCA) nur die 3 gefundenen relevanten Hauptkomponenten verwende und außerdem in dieses System Fehlergrößen verschiedenen Ausmaßes einstreue.

 

Das Beispiel als solches erscheint mir allerdings für die Beschreibung der Vorgänge der FA/PCA etwas seltsam gewählt: während die FA/PCA ja eigentlich dafür konzipiert ist, additive Kompositionen aufzudecken, also z.B.

 

      x1 = a1*f1 + b1*f2

      x2 = a2*f1 + b2*f2

      x3 = a3*f1 + b3*f2

 

wobei f1,f2 die unbekannten Werte der zugrundeliegenden Faktoren, und x1,x2,x3,... die Werte der "empirisch" beobachteten, durch die unbekannten Faktorenwerte zusammengesetzten, Variablen enthalten, wird hier mit multiplikativen* Kompositionen gearbeitet, z.B.

 

   x1 = f1*f2

   x2 = f1*f3

   x3 = f2*f3

   x4 = f1*f2*f3

 

         wobei f1=länge, f2=breite, f3 = Höhe

 

als Zufallswerte synthetisch erzeugt werden und in einer echten Faktorenanalyse als Faktoren durch die Messungen von Volumen, Oberfläche etc wiedergefunden werden sollen.

 

Eigentlich wird hier also die Faktorenanalyse auf das gestützt, was wir in Regression und Anova-Modellen als "Interaktionsterme" bezeichnen; diese Art von Modell für die FA/PCA, und insbesondere die vollständige Modellierung durch diese Interaktionsterme erscheint mir aber als sehr ungewöhnlich, jedenfalls habe ich in allen meinen Arbeiten damit solche Modelle noch nie betrachtet.

Interaktionsterme sind zwar in der Regression und in der Anova relativ üblich (z.B. in SPSS einfach zu modellieren) -wenn auch eher als zusätzliche Option- , aber als Items in der FA/PCA ? Das würde mich jetzt einmal interessieren.

 

Hat jemand hier mehr Erfahrung damit ? (just curious!)

 

 

Gottfried

 

 

 

 

 

 

 

 

 

 

 

 

Anhang:

Ich habe mal neugierigerweise dieses Modell "linearisiert", indem ich die berechneten Werte für die x1,x2,x3,... logarithmiert habe und somit die Produkte in Summen (wie von der FA/PCA erwartet) verwandelt.

 

Da dies auch bedeutet, die Daten als ratio-skaliert zu verstehen (die Position des Nullpunkt ist nicht trivial) habe ich die Daten dann auf den Nullpunkt zentriert indem ich einfach den Datensatz verlängert habe mit den jeweils negativen Werten der "Messungen" in x1,x2,.... so daß für jede Variable der Mittelwert auf Null geht.

 

Mit solcherart transformierten Werten erhalte ich dann

 

                *  überraschenderweise sehr hohe Korrelationen der Items untereinander,

 

aber nichtsdestotrotz via multipler Regression

 

                * eine perfekte Reproduktion der zugrundeliegenden Komposition

                  über die unstandardisierten beta-Gewichte

 

Ergebnisse:

 

* Regressionsmodell (via PCA über Kovarianzmatrix, Rohdaten zu Logarithmen transformiert):

 

 unstandardisierte beta-Werte

* Dependent items (as compositions of the independents):

                x1=Vol                  1.000    1.000    1.000                    keine Residualvarianz

                x2=Ofl                    0.799    0.740    0.993                    eine kleine Menge Residualvarianz

                x3=L*B                  1.000    1.000    0.000                    keine Residualvarianz

                x4=L*H                 1.000    0.000    1.000                    keine Residualvarianz

                x5=B*H                 0.000    1.000    1.000                    keine Residualvarianz

                --------------------------------------------------------------------------------------

* Independent items  (explaining the dependent items):

                f1=L                        1.            0.            0.

                f2=B                       0.            1.            0.

                f3=H                       0.            0.            1.

               

 

Aber dies nur am Rande.

 

Übrigens hat dann - als einzige- die Variable x2 (="Ofl") einen weiteren (kleinen) Varianzanteil da hier die Logarithmierung einer Summe  Ofl = 2∙(f1 ∙ f2+f2 ∙ f3 + ...) eine zusätzliche (wenn auch kleine) Nichtlinearität hinzubringt.

 

 

 

 

 

 

 

 

 

Kennwerte (aus dem angegebenen Datensatz reproduziert)

 

Der angegebene Datensatz (Kopie siehe Ende des Dokuments) ist das zweite Beispiel (...q02) mit eingestreuten Fehlern unter http://www.sgipt.org/wisms/fa/Quader/q02.htm

Korrelationsmatrix:

Neu berechnet aus angegebenen Rohdaten

Dokumentiert in (1)

 

 

 

 

L

B

H

Vol

OFl

L∙B

L∙H

B∙H

L

  1.

 -0.0983

  0.1007

  0.5455

  0.5608

  0.6258

  0.7143

  0.0523

B

 -0.0983

  1.

  0.1207

  0.4734

  0.5368

  0.6079

  0.0566

  0.7051

H

  0.1007

  0.1207

  1.

  0.6015

  0.6562

  0.2085

  0.6970

  0.6972

Vol

  0.5455

  0.4734

  0.6015

  1.

  0.9715

  0.8346

  0.8149

  0.7707

OFl

  0.5608

  0.5368

  0.6562

  0.9715

  1.

  0.8405

  0.8380

  0.8116

L∙B

  0.6258

  0.6079

  0.2085

  0.8346

  0.8405

  1.

  0.5792

  0.5398

L∙H

  0.7143

  0.0566

  0.6970

  0.8149

  0.8380

  0.5792

  1.

  0.4827

B∙H

  0.0523

  0.7051

  0.6972

  0.7707

  0.8116

  0.5398

  0.4827

  1.

 

Die aus den dokumentierten Rohdaten berechnete Korrelationsmatrix ist positiv definit mit einem kleinsten Eigenwert weit genug von dem Maschinen-epsilon entfernt, so daß auch die Cholesky-Dekomposition problemlos mit genügend Stellen Genauigkeit möglich ist.

 

Original data with  17, input read with  17, computet with 19,

 and showed with  3 digit accuracy

(for control here the analysed original matrix):

 

Läng  Breit  Höhe  Volum Ober  L*B   L*H   B*H

 1    -.099  .102  .551  .566  .632  .721  .053

-.099  1     .122  .478  .542  .614  .057  .712

 .102  .122  1     .608  .663  .211  .704  .704

 .551  .478  .608  1     .981  .843  .823  .779

 .566  .542  .663  .981  1     .849  .846  .82

 .632  .614  .211  .843  .849  1     .585  .545

 .721  .057  .704  .823  .846  .585  1     .488

 .053  .712  .704  .779  .82   .545  .488  1

 

 The matrix is not positive definit. Cholesky decomposition is not success-

 

 

Anmerkung: es ist überraschend, daß es überhaupt möglich sein soll, aus dem Produkt des (z-standardisierten) Rohdatensatzes Z mit sich selbst überhaupt eine nicht positiv-semidefinite Korrelationsmatrix zu erzeugen. Hier müssen gravierende Rundungsfehler unterlaufen sein!

 

Eigenwerte:

 

Wert

Log10(wert)

 

dokumentiert in (1)

Ev1

  5.04807735

  0.70312600

 

5.08905

Ev2

  1.52701773

  0.18384408

 

1.53238

Ev3

  1.13576922

  0.05529010

 

1.1371_

Ev4

  0.11533442

 -0.93804107

 

.1064_

Ev5

  0.10071085

 -0.99692372

 

.09161

Ev6

  0.06805516

 -1.16713892

 

.05861

Ev7

  0.00500776

 -2.30035672

 

-5.07D-3

Ev8

  0.00002750

 -4.56066522

 

-.01008

Anm.: die Korrelationsmatrix im Original (1) oder die Eigenwertanalyse muß mit großer numerischer Ungenauigkeit gerechnet worden sein: durch die Konstruktion der Berechnungsweise einer Korrelationsmatrix können negative Eigenwerte bei reellen Rohdaten (bei genügender numerischer Genauigkeit beim Rechnen) nicht entstehen.

 

 

 

Cholesky-Ladungsmatrix:

 

f1

f2

f3

f4

f5

f6

f7

f8

 

 Diagonaleinträge
dokumentiert in (1)

L

         1.

  .

  .

  .

  .

  .

  .

  .

 

1    _

B

 -0.0983

  0.9952

  .

  .

  .

  .

  .

  .

 

.9951

H

  0.1007

  0.1312

  0.9862

  .

  .

  .

  .

  .

 

.9859

Vol

  0.5455

  0.5296

  0.4838

  0.4336

  .

  .

  .

  .

 

.4149

OFl

  0.5608

  0.5948

  0.5289

  0.2186

  0.0650

  .

  .

  .

 

-.011_

L∙B

  0.6258

  0.6726

  0.0580

  0.2515

  0.0585

  0.2931

  .

  .

 

-.6477

L∙H

  0.7143

  0.1274

  0.6169

  0.1370

  0.0836

 -0.0976

  0.2404

  .

 

-.9996

B∙H

  0.0523

  0.7137

  0.6066

  0.1632

  0.0186

 -0.1716

 -0.2513

  0.0158

 

-1.1287

Anm.: betreffs der negativen Diagonaleinträge in (1) siehe Anm. zu Korrelationen und Anm. zu Eigenwerten.

 

Die ersten 3 Hauptkomponenten:

 

hier berechnet

 

dokumentiert in (1)

 

PC1

PC2

PC3

 

PC1*

PC2*

PC3*

L

  0.5613

 -0.7370

 -0.3142

 

.563

-.738

-.314

B

  0.5313

  0.7243

 -0.3942

 

.533

.725

-.395

H

  0.6639

  0.0634

  0.7264

 

.667

.064

.727

Vol

  0.9725

 -0.0291

 -0.0271

 

.976

-.029

-.027

OFl

  0.9996

  0.0031

 -0.0086

 

1.004

3D-3

-9D-3

L∙B

  0.8372

 -0.0282

 -0.5063

 

.841

-.028

-.507

L∙H

  0.8400

 -0.4456

  0.2402

 

.843

-.446

.24

B∙H

  0.8115

  0.5050

  0.1979

 

.815

.506

.198

Anm.: (*) = dokumentiert in (1)

 

 

hier berechnet

dokumentiert in (1)

 

Reproduzierte Korrelationsmatrix basierend auf 3 Hauptkomponenten:

 

L

B

H

Vol

OFl

L∙B

L∙H

B∙H

L

  0.9569

 -0.1118

  0.0977

  0.5758

  0.5615

  0.6497

  0.7244

  0.0211

B

 -0.1118

  0.9623

  0.1123

  0.5063

  0.5367

  0.6240

  0.0289

  0.7189

H

  0.0977

  0.1123

  0.9725

  0.6241

  0.6576

  0.1862

  0.7039

  0.7145

Vol

  0.5758

  0.5063

  0.6241

  0.9474

  0.9723

  0.8287

  0.8234

  0.7691

OFl

  0.5615

  0.5367

  0.6576

  0.9723

  0.9993

  0.8411

  0.8362

  0.8110

L∙B

  0.6497

  0.6240

  0.1862

  0.8287

  0.8411

  0.9580

  0.5942

  0.5650

L∙H

  0.7244

  0.0289

  0.7039

  0.8234

  0.8362

  0.5942

  0.9619

  0.5042

B∙H

  0.0211

  0.7189

  0.7145

  0.7691

  0.8110

  0.5650

  0.5042

  0.9528

 

 

 

Reproduktionsmatrix aus 3 Faktoren:

 

 

 .961 -.111  .1    .58   .566  .654  .729  .023

-.111  .967  .115  .51   .541  .628  .031  .724

 .1    .115  .977  .629  .663  .19   .709  .719

 .58   .51   .629  .955  .98   .835  .83   .775

 .566  .541  .663  .98  1.007 .848  .843  .818

 .654  .628  .19   .835  .848  .964  .6    .57

 .729  .031  .709  .83   .843  .6    .968  .509

 .023  .724  .719  .775  .818  .57   .509  .959

 

 

 

Fehler:

 

L

B

H

Vol

OFl

L∙B

L∙H

B∙H

L

  0.0431

  0.0135

  0.0030

 -0.0304

 -0.0007

 -0.0239

 -0.0101

  0.0312

B

  0.0135

  0.0377

  0.0085

 -0.0329

  0.0001

 -0.0161

  0.0277

 -0.0138

H

  0.0030

  0.0085

  0.0275

 -0.0225

 -0.0014

  0.0223

 -0.0069

 -0.0173

Vol

 -0.0304

 -0.0329

 -0.0225

  0.0526

 -0.0008

  0.0059

 -0.0085

  0.0016

OFl

 -0.0007

  0.0001

 -0.0014

 -0.0008

  0.0007

 -0.0007

  0.0017

  0.0005

L∙B

 -0.0239

 -0.0161

  0.0223

  0.0059

 -0.0007

  0.0420

 -0.0150

 -0.0252

L∙H

 -0.0101

  0.0277

 -0.0069

 -0.0085

  0.0017

 -0.0150

  0.0381

 -0.0214

B∙H

  0.0312

 -0.0138

 -0.0173

  0.0016

  0.0005

 -0.0252

 -0.0214

  0.0472

 

 

 

Residualanalyse Original-Korrelationen und aus 3 Faktoren reproduzierte:

 .039  .012  1D-3  .029  0     .022  8D-3  .029

 .012  .033  7D-3  .032  1D-3  .014  .026  .011

 1D-3  7D-3  .023  .022  0     .02   4D-3  .015

 .029  .032  .022  .045  1D-3  8D-3  7D-3  3D-3

 0     1D-3  0     1D-3  7D-3  1D-3  3D-3  2D-3

 .022  .014  .02   8D-3  1D-3  .036  .015  .025

 8D-3  .026  4D-3  7D-3  3D-3  .015  .032  .021

 .029  .011  .015  3D-3  2D-3  .025  .021  .041

 

Anm.: in der Residualtabelle sollte der rot-markierte Wert negativ sein; das Softwareprogramm scheint hier Fehler zu haben oder einfach alle Residuen als absolute Werte zu dokumentieren.

 

 

Statistiken über wiederholte Zufallsexperimente mit hinzugefügten Fehlern

 

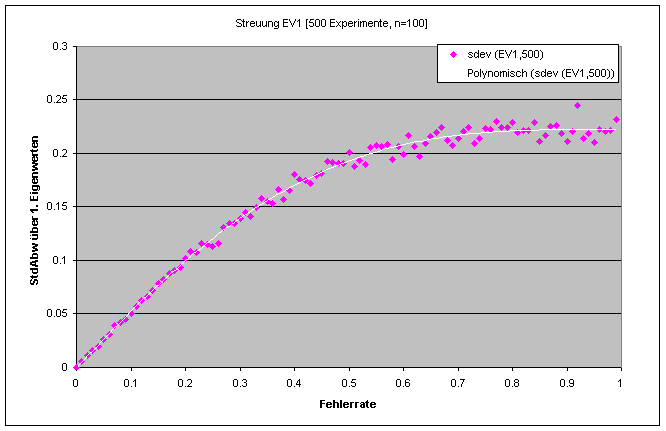
Mit Fehlerraten a zwischen 0 und 2 (als relativer normalverteilter Fehler den Rohdaten hinzugefügt) in Schritten von 0.1 wurden mit jeder Fehlerrate 50 Experimente mit (jeweils neuen) Zufallsfehlern durchgeführt.

Die durchschnittlichen Größen der jeweiligen ersten Eigenwerte sowie deren Streuungen werden im folgenden grafisch dokumentiert.

 

Die kontinuierlichen Linien entstehen durch kubische Interpolationssplines der Software Excel. Für die durchschnittlichen Werte der EV1 wurden außerdem die 95% Konfidenzintervalle für die Inferenz auf eine ideale Population von Versuchen ausgewiesen (hier ist simpel der SEMean verwendet worden, möglicherweise empfiehlt sich in einer genaueren Untersuchung ein besserer Streuungskoeffizient!).

 

Berechnungsmodus für einen Datenpunkt xa,r,c: mit der Fehlerrate a:  xa,r,c = xr,c ∙(1+ a∙Normal(0,1))   wobei r den Zeilenindex und c den Spaltenindex der Datentabelle bezeichnen.

 

 

 

 

 

 

 

Anm.: Fehlerraten von 1 (und höher) heißt hier, daß die Originaldaten durch Fehler derselben Größenordnung wie sie selbst überlagert werden; die entsprechenden Korrelationsmatrizen und die Eigenwertverläufe sollten sich deshalb denen von reinen Zufallsdaten annähern. Eine weitere Steigerung der Streuung der jeweils ersten Eigenwerte (bei hier 50 Sample-Ziehungen) ist ab einer relativen Fehlerrate von a>1 oder anscheinend bereits bei a>0.6 deshalb nicht zu erwarten. Deutlicher wird das in den Grafiken für 500 Ziehungen pro Fehlerrate, weshalb hier die x-Achse auf das Intervall 0..1 gekürzt werden konnte.

 

Gottfried Helms, 31.10.2014

 

 

Daten

 

Die Daten entstehen durch einen Zufallsdatensatz  der drei "unabhängigen" Items Länge, Breite, Höhe jeweils zwischen 0 und 100; hiervon abgeleitet sind Vol=L∙B∙H, OFl= 2(L∙B + L∙H + B∙H), und deren Einzelkomponenten L∙B, L∙H, B∙H . Diesen (fixierten) Werten (als konstante Datenbasis für alle Experimente in http://www.sgipt.org/wisms/fa/Quader/q00.htm verfügbar) wird bei jeder "Ziehung" ein relativer Fehler mit der Rate a überlagert. Aus 10, 30, 50 oder mehr Ziehungen mit demselben Parameter a wird dann der durchschnittliche erste Eigenwert berechnet. Soweit ich die Erklärungen in der Webseite verstanden habe, läuft es hierbei auf die Formel

 

                xa,r,c = xr,c∙(1+a∙Normal(0,1))                     wobei r den Zeilenindex und c den Spaltenindex der folgenden Tabelle bezeichnen

 

hinaus, wobei der Zufallsgenerator Normal(0,1)=Normal(mean,stddev) möglicherweise in einer Weise gestutzt wird, daß es wohldefinierte minimale und maximale Werte gibt.

Für die eigene Statistik mit variablen Fehlerraten a wurde der unverzerrte Datensatz herangezogen und für jede "Ziehung" erneut zufällige Fehler darauf gerechnet.

 

Datensatz in der Version ("...q02" mit Fehlerüberlagerung), kopiert aus Webpage http://www.sgipt.org/wisms/fa/Quader/q02.htm :

 

Lfd. Nr

L

B

H

Vol

Ofl

L∙B

L∙H

B∙H

1

0.995

94.203

61.759

5839.5

11997

94

62

5819.8

2

2

65.4

70.9

9192.8

9764

130.3

141.97

4609.5

3

3

19

39.1

2229.6

1831.3

57.3

116.83

739.32

4

4.01

69.98

91.37

25646

14170

279.1

366.11

6456.1

5

5

84.6

8

3393.1

2293.5

424.95

39.97

680.62

6

6

97.13

72.52

42348

16152

579.01

438.73

7041.4

7

7

45.9

45

14575

5384.1

322.41

312.98

2068.6

8

8

19

75.4

11367

4385.5

151.79

598.06

1426.4

9

9

13

85.9

10067

4039.8

117.19

772.99

1118.6

10

10

58.3

38.8

22662

6462.6

579.42

388.69

2258

11

11

13

70.7

10149

3696.6

143.22

781.77

919.96

12

11.97

1

58.9

709.45

1552.6

12.1

709.36

59.02

13

12.97

41.25

72.72

39012

8967.7

531.59

948.95

2988.6

14

14

32.1

20.1

8984.1

2716

447.23

281.37

639.43

15

14.9

81.7

33.82

41533

9073.9

1231.1

510.03

2781.9

16

15.9

19

29

8777.3

2627.6

304.91

463.44

552.08

17

16.99

96.87

56.98

93719

16390

1654.3

966.7

5533.3

18

18

72

53

69195

12114

1292.9

958.57

3778.4

19

19.1

87.2

42.9

71005

12480

1648.7

818.62

3745.7

20

20

79

38.1

60030

10706

1586.4

762.56

3009.8

21

21

54.1

48.7

55591

9604.8

1135.9

1029.1

2657

22

22

82.2

19

34111

7522.9

1811.4

415.92

1559.2

23

23

40.2

55.1

50306

8771.8

924.69

1267.8

2197.8

24

23.9

73.9

73.1

129923

17887

1779

1749

5405.9

25

25.1

79

49.9

98788

14308

1974.1

1244.6

3962.8

26

26

79.7

40.1

83391

12635

2070.5

1036.8

3211.4

27

26.9

46

2

2487.2

2779.6

1247.8

54

92.1

28

28

53

42

62189

9783.6

1486.2

1181.6

2241

29

29.1

32.1

52

48267

8241.3

930.8

1501.2

1664.9

30

30.2

35.9

79.9

86536

12669

1082.4

2403.1

2881.8

31

31.1

77.9

79

191451

22190

2423.5

2459.8

6181.2

32

31.9

64.3

68.1

139557

17054

2046.2

2168.3

4364.9

33

32.9

44

12

17365

4729

1446.9

396.48

527.39

34

34.03

59.94

67.01

136942

16665

2036.4

2278.9

4025.5

35

35

6

91.1

19030

7872.3

209.84

3181.1

545.4

36

36.05

57.98

25.91

54349

9032.8

2097.8

935.39

1507.1

37

36.9

91.4

26.9

92248

13693

3429.6

998.3

2484.1

38

37.7

16

25

15150

3914.6

610.5

955.26

402.52

39

38.98

71.67

9.02

25344

7631.4

2796.2

350.83

648.09

40

39.93

67.26

48.13

128831

15633

2688.6

1931.9

3215.3

41

40.8

51.7

31.2

66014

9995.4

2143.4

1272.6

1611.4

42

41.8

33.9

46.2

65479

9891.6

1430

1929.4

1577

43

42.8

15

6

3866.5

1995.4

646.66

256.75

89.37

44

43.69

75.92

14.09

47055

10072

3338.2

614.08

1061.2

45

45.1

95.2

100.36

427569

36505

4260.7

4503.1

9512.1

46

46

97.6

74.8

338064

30459

4504.3

3465.3

7352.1

47

47

75

39.9

140990

16757

3515.4

1883

2993.1

48

48.2

24.8

21

25168

5468

1210.2

1014.2

522.96

49

48.87

47.03

38.16

87468

11923

2299.2

1871

1777.6

50

49.5

90.7

12

54845

12492

4546.9

598.39

1092.2

51

50.7

83.6

84.9

365753

31525

4283.4

4325

7142.9

52

52

49.1

54.2

138096

15947

2540.9

2806.3

2648.4

53

52.9

91.6

19.9

96975

15529

4887.4

1062.4

1838.1

54

54

43

8

18639

6205.5

2318.1

433.41

345.32

55

55.11

95.44

68.29

359308

31104

5283.9

3745.5

6532.2

56

56.2

86.6

64.4

312059

27985

4873.1

3589.4

5587.8

57

57.1

64.1

67.2

244645

23553

3646.7

3821.6

4279.6

58

57.8

98.1

84.2

475935

37706

5727.3

4844.4

8271.2

59

59.3

90.2

25

132362

18095

5295.2

1476.3

2243.8

60

60.1

9

12.1

6463

2739.8

542

718.57

107.12

61

61.17

35.99

63.98

140622

16952

2186.4

3903.6

2296.5

62

62.2

55.2

25.9

88211

12882

3433.3

1613.5

1419.3

63

63

83.4

22

115059

16788

5239.4

1391.5

1819.8

64

64

59.9

89.4

341463

29893

3855.1

5687.6

5328.1

65

65.1

53.8

23.1

80424

12477

3515.6

1492

1241.1

66

65.9

35.9

38.1

90788

12528

2370

2507.6

1366.8

67

67.2

13

20.1

17488

4926.4

872.78

1337.1

260.27

68

68.06

78.08

68.41

364870

30714

5282.5

4677.5

5447.4

69

69

80.1

84.2

464248

35996

5512.2

5791

6753.9

70

70.2

45.7

45.1

144287

16847

3224.4

3154.2

2058.9

71

70.8

38.1

82

222377

23333

2693.5

5829.9

3114

72

72.4

4

68.9

19880

11060

289.05

4994.3

275.5

73

73.14

51.87

38.13

144579

17101

3784

2762.6

1979.1

74

73.7

60.9

67.1

302865

27091

4516

4945

4069.3

75

75.3

81.7

95.6

593395

42470

6115.9

7156.3

7870.9

76

75.9

7

95.5

50468

16849

532.85

7200.6

665.79

77

76.81

78.84

45.72

280449

26490

6070.2

3531.8

3630.3

78

78

12

21

19557

5640.3

939.57

1639.3

253.48

79

78.95

40.02

100.07

316446

29963

3157.6

7905.7

3986.5

80

79.6

51.1

99.3

408737

34388

4064.8

8024.3

5129.6

81

81

4

23

7470.8

4552.3

323.47

1860.5

92.2

82

82.2

56.1

52.2

240217

23617

4606.2

4252.9

2903.7

83

82.7

78.8

98.3

640215

44866

6538.9

8105.2

7726.1

84

83.7

75

60

376680

31771

6315

5038.5

4488.7

85

84.8

3

17

4353.7

3514

255.25

1446.7

50.8

86

86

72.1

31.9

197609

22588

6191

2751.4

2301.2

87

87.2

95.9

40.9

343067

31644

8338.8

3563.9

3931.2

88

87.6

31.1

76.9

210247

23745

2739.6

6815.8

2395.3

89

89.4

64.9

13.1

75274

15629

5776.3

1160.3

846.53

90

90.29

41.84

92.76

352882

32026

3778.3

8414.4

3918

91

90.9

54

69.4

339522

29850

4899.4

6260.6

3707.8

92

92.2

9

2

1646.4

2061.2

829.44

184.08

18.02

93

93.4

53.14

98.91

487931

38467

4923.4

9204.6

5223.8

94

94.1

24.1

23.2

52222

9977.7

2254.2

2163.6

552.84

95

94.58

47

24.99

111323

16045

4450.6

2361.8

1176.1

96

96.2

1

59.3

5687.1

11636

96

5645.6

59.1

97

96.3

96.7

85.2

793775

51747

9364.4

8316.5

8259.3

98

97.9

92.1

65.1

581293

42819

8993.7

6365.1

5975.7

99

98.4

26.9

72.1

192615

23405

2672.5

7160.2

1947.3

100

99.9

47.2

83.9

393740

34157

4703.5

8371.5

3957.8