|
|
|
Variations on a
well known generalized infinite continued fraction
with a simple pattern
Rational or transcendental values by
change of offset
of a simple pattern
Preface: all the following is an amateurish heuristic and rediscovery. A thorough discussion of this matter was already lead by David Angell in [1], which I found when checked the occuring sequences of numbers in [OEIS] .
Observations and discussion
The "generalized continued fraction" (gcf) allows non-unit-values on the numerators of the partial fractions. Here that coefficients are denoted as b with index k, where the index begins at zero and the gcfs are assumed to have a nonterminating sequence of coefficients:
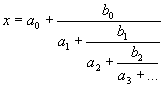
Some such continued fractions having coefficients with a simple pattern are well known, for instance[1]:
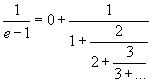
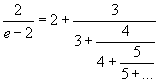
Interestingly, with various offsets of that pattern we can get rational values instead of compositions of the transcendend value of e:
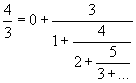
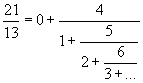
In the following I provide a table with some heuristics (thanks to the "wolfram alpha" team; I used their www-based engine[2] for most of the compositions involving the exponentials).
Denote CF([a0, a1, a2, …],[b0, b1, b2, …]) the generalized continued fraction. Now let the ak and bk be defined by simple functions f(k) and g(k) of the index k.:
xf,g = CF( [ak = f(k) ] , [ bk = g(k) ] )
For instance, to obtain 1/(e-1) we write
1/(e-1) = CF( [ak = k ] , [ bk = 1+k ] )
The following table gives the heuristics for a family of continued fractions having different offsets. The rows define the varying offsets for the computation of b-coefficients in the function bk =foffset(k) = offset+k , the columns the according varying offsets for the computation of the a-coefficients.
Example: the entry in row "2+k" and column "3+k" means x=CF([3,4,5,...][2,3,4,...]) and heuristically we find x = – (2*e – 5)/(4*e – 11) , where e=exp(1):
Table 1:
|
b\a |
0+k |
1+k |
2+k |
3+k |
4+k |
5+k |
… |
|
0+k |
0 |
1 |
2 |
3 |
4 |
5 |
… |
|
1+k |
|
|
|
|
|
|
… |
|
2+k |
1 |
|
|
|
|
|
|
|
3+k |
4 |
2*1 |
|
|
|
|
|
|
4+k |
3*7 |
3*3 |
3*1 |
|
|
|
|
|
5+k |
4*34 |
4*13 |
4*2*2 |
4*1 |
|
|
|
|
6+k |
5*209 |
5*73 |
5*3*7 |
5*5 |
5*1 |
|
|
|
7+k |
6*1546 |
6*501 |
6*4*34 |
6*31 |
6*6 |
6*1/1 |
|
|
8+k |
|
|
|
7*229 |
7*43 |
7*7/8 |
|
|
9+k |
|
|
|
8*1061 |
8*358 |
8*57/73 |
|
|
r+1+k |
n(r+1) |
|
|
|
|
|
|
By the construction of the simple pattern it is obvious, that the diagonal and subdiagonals form the sequences of convergents of one similar pattern; so if we look at for instance row "8+k" and column "5+k" and follow the diagonal up to the top we find:
beginning
at xk = 7*7/8 = 6+1/8 = 49/8
then xk-1 = 4+7/(7*7/8)= 4 + 8/7 = 36/7
then xk-2 = 3+6/(36/7) = 3+7/6 = 25/6
then xk-3 = 2+5/(25/6) = 2+6/5 = 16/5
then xk-4 = 1+4/(16/5) = 1+5/4 = 9/4
then xk-5 =0+3/(9/4) = 0+4/3 = 4/3
which proceeds along the subdiagonal 3 to arrive at x=4/3
It may be easier to follow the opposite direction: if we start at some entry in the first column and travel along the according diagonal, we find the simple arithmetic progressions in the numerators (nurow,col) and denominators (derow,col) the same way. Example: we begin at (row,col)= (4,0).
nu4,0
= 3*7 de4,0
= 13 = 7 + 6
nu5,1 = 4*13 =
4*de4,0 de5,1
= 21 = de4,0+8
nu6,2 = 5*21 =
5*de5,1 de6,2
= 31 = de5,1+10
nu7,3 = 6*31 =
6*de6,2 de7,3
= 43 = de6,2+12
nuk,k-4 = (k-1)*dek-1,k-5 dek,k-4 = dek-1,k-5+2*(k-1)
=(k-1)+(k-1)2(k-2) = 1 +
k(k-1)
=k3–4k2+6k–3 = k2 – k + 1
For the first column a recurrence-formula for the r+1'th numerator (nr+1) and denominator (dr+1) seems to be
nr+1
= r*dr + r*nr
dr+1 = r*dr
+ 1*nr
or in a matrix-formula:
![]()
so for the entry nr+1/dr+1 at row "5+k" and col "0+k" has r=4 and
4*34/73 = (4* 13 + 4*21) / (4*13 + 1*21)
where 13 and 21 are taken from the denominator and numerator of the previous entry.
The function in Pari/GP:
\\ for funcA and funcB give the formula of a functions-definition
\\ f(k)=<formula>
\\ as strings. for instance CF("2","1") evaluates CF([2,2,2,2,…],[1,1,1,1…])
\\ as strings. for instance CF("1+k","2+k") evaluates CF([1,2,3,4,…],[2,3,4,5…])
{CF(funcA,funcB="1",maxcoeffs=100) = local(convgts,a_k,b_k);
eval(Str("f(k)=",funcA));
eval(Str("g(k)=",funcB));
convgts = matid(2);
for(k=0,maxcoeffs-1, a_k =f(k);b_k=g(k); convgts= convgts*[0,1; b_k,a_k]);
return( convgts[2,2]/ convgts[1,2]*1.0) };
\p 200
\\ Example-computation
result = CF("2+k","1+k") \\ = 1/(2*e - 5)
The sequences of numerators and denominators are known in the OEIS, for instance we find for the first column in the table
numerator: 1,4,21,136,… http://www.research.att.com/~njas/sequences/A052852
denominator 1,3,13,73,… http://www.research.att.com/~njas/sequences/A000262
A000262 Number of "sets of lists": number of partitions of {1,..,n} into any number of lists, where a list means an ordered subset.
A052852 E.g.f.: (x/(1-x))*exp(x/(1-x))
A simple grammar. Number of {121,212}-avoiding n-ary words of length n.
- R. Stephan, Apr 20 2004
Contribution from David Angell (angell(AT)maths.unsw.edu.au), Dec 18 2008:
(Start)
If n is a positive integer then the infinite continued fraction (1+n)/(1+(2+n)/(2+(3+n)/(3+...)))
converges to the rational number A052852(n)/A000262(n).
(End)
The following columns can be retrieved as well. The common aspect is, that the sequences are formed by the generating function for exp(x/(1–x)) divided by some powers of (1-x).
Gottfried Helms, 28.03.2010, textversion 1.2
Links and references
