Asymptotic factorizations of an Eulerproduct into primefactors

Asymptotic factorizations of an Eulerproduct into primefactors.

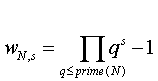Let : : where the q are prime. We are considering lim_N->oo w_N,s (mod p_k) where the p_k are primes and here p_k=2...89

and estimate the relative frequency of primefactors p_k after evaluating the euler-product w_N,s with exponent s up to the Nth prime.

Tables: absolute and (scaled) relative count of occurences of primefactor p_k in relation to N, formula: rel=(count/N) * (p_k-1)²

N=200	Count of occurences of primefactor p in the (partial) Eulerproduct over prime(1)...prime(200)
s\p	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73	79	83	89
1	392	142	61	35	20	17	12	9	10	6	4	3	3	4	5	3	4	3	1	2	3	1	4	2
2	784	294	114	71	40	35	23	20	17	12	11	8	7	10	9	6	6	6	3	4	4	4	6	2
3	392	238	61	107	20	50	12	35	10	6	18	14	3	12	5	3	4	7	8	2	10	5	4	2
4	983	294	245	71	40	75	48	20	17	27	11	18	16	10	9	13	6	13	3	4	8	4	6	6
5	392	142	110	35	107	17	12	9	10	6	32	3	21	4	5	3	4	14	1	14	3	1	4	2
6	784	493	114	224	40	104	23	69	17	12	40	28	7	28	9	6	6	17	15	4	18	13	6	2
7	392	142	61	67	20	17	12	9	10	54	4	3	3	31	5	3	4	3	1	18	3	1	4	2
8	1182	294	245	71	40	75	99	20	17	27	11	18	38	10	9	13	6	13	3	4	16	4	6	15
9	392	334	61	107	20	50	12	105	10	6	18	52	3	12	5	3	4	7	8	2	24	5	4	2
10	784	294	208	71	217	35	23	20	17	12	69	8	50	10	9	6	6	33	3	28	4	4	6	2
11	392	142	61	35	39	17	12	9	98	6	4	3	3	4	5	3	4	3	36	2	3	1	4	24
12	983	493	245	224	40	216	48	69	17	27	40	61	16	28	9	13	6	37	15	4	34	13	6	6
	relative frequency: count/N*(p_k - 1)²
1	1.96	2.84	4.88	6.30	10.00	12.24	15.36	14.58	24.20	23.52	18.00	19.44	24.00	35.28	52.90	40.56	67.28	54.00	21.78	49.00	77.76	30.42	134.48	77.44
2	3.92	5.88	9.12	12.78	20.00	25.20	29.44	32.40	41.14	47.04	49.50	51.84	56.00	88.20	95.22	81.12	100.92	108.00	65.34	98.00	103.68	121.68	201.72	77.44
3	1.96	4.76	4.88	19.26	10.00	36.00	15.36	56.70	24.20	23.52	81.00	90.72	24.00	105.84	52.90	40.56	67.28	126.00	174.24	49.00	259.20	152.10	134.48	77.44
4	4.92	5.88	19.60	12.78	20.00	54.00	61.44	32.40	41.14	105.84	49.50	116.64	128.00	88.20	95.22	175.76	100.92	234.00	65.34	98.00	207.36	121.68	201.72	232.32
5	1.96	2.84	8.80	6.30	53.50	12.24	15.36	14.58	24.20	23.52	144.00	19.44	168.00	35.28	52.90	40.56	67.28	252.00	21.78	343.00	77.76	30.42	134.48	77.44
6	3.92	9.86	9.12	40.32	20.00	74.88	29.44	111.78	41.14	47.04	180.00	181.44	56.00	246.96	95.22	81.12	100.92	306.00	326.70	98.00	466.56	395.46	201.72	77.44
7	1.96	2.84	4.88	12.06	10.00	12.24	15.36	14.58	24.20	211.68	18.00	19.44	24.00	273.42	52.90	40.56	67.28	54.00	21.78	441.00	77.76	30.42	134.48	77.44
8	5.91	5.88	19.60	12.78	20.00	54.00	126.72	32.40	41.14	105.84	49.50	116.64	304.00	88.20	95.22	175.76	100.92	234.00	65.34	98.00	414.72	121.68	201.72	580.80
9	1.96	6.68	4.88	19.26	10.00	36.00	15.36	170.10	24.20	23.52	81.00	336.96	24.00	105.84	52.90	40.56	67.28	126.00	174.24	49.00	622.08	152.10	134.48	77.44
10	3.92	5.88	16.64	12.78	108.50	25.20	29.44	32.40	41.14	47.04	310.50	51.84	400.00	88.20	95.22	81.12	100.92	594.00	65.34	686.00	103.68	121.68	201.72	77.44
11	1.96	2.84	4.88	6.30	19.50	12.24	15.36	14.58	237.16	23.52	18.00	19.44	24.00	35.28	52.90	40.56	67.28	54.00	784.08	49.00	77.76	30.42	134.48	929.28
12	4.92	9.86	19.60	40.32	20.00	155.52	61.44	111.78	41.14	105.84	180.00	395.28	128.00	246.96	95.22	175.76	100.92	666.00	326.70	98.00	881.28	395.46	201.72	232.32

																									113

N=1000	Count of occurences of primefactor p in the (partial) Eulerproduct over prime(1)...prime(1000)
s\p	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73	79	83	89
1	1961	736	307	191	110	85	65	50	48	33	31	28	24	24	23	17	19	17	18	13	14	13	11	12
2	3952	1494	613	385	219	173	129	110	96	68	67	54	48	48	44	36	35	30	34	27	24	25	21	21
3	1961	1226	307	573	110	261	65	175	48	33	103	88	24	73	23	17	19	54	50	13	42	40	11	12
4	4951	1494	1253	385	219	356	265	110	96	144	67	107	97	48	44	74	35	65	34	27	49	25	21	45
5	1961	736	552	191	545	85	65	50	48	33	176	28	124	24	23	17	19	83	18	69	14	13	11	12
6	3952	2493	613	1160	219	527	129	349	96	68	205	165	48	142	44	36	35	98	95	27	79	78	21	21
7	1961	736	307	356	110	85	65	50	48	258	31	28	24	166	23	17	19	17	18	98	14	13	11	12
8	5950	1494	1253	385	219	356	523	110	96	144	67	107	200	48	44	74	35	65	34	27	103	25	21	81
9	1961	1716	307	573	110	261	65	513	48	33	103	262	24	73	23	17	19	54	50	13	119	40	11	12
10	3952	1494	1104	385	1090	173	129	110	96	68	347	54	253	48	44	36	35	166	34	138	24	25	21	21
11	1961	736	307	191	211	85	65	50	510	33	31	28	24	24	23	17	19	17	176	13	14	13	11	129
12	4951	2493	1253	1160	219	1080	265	349	96	144	205	334	97	142	44	74	35	202	95	27	163	78	21	45
	relative frequency: count/N*(p_k - 1)²
1	1.96	2.94	4.91	6.88	11.00	12.24	16.64	16.20	23.23	25.87	27.90	36.29	38.40	42.34	48.67	45.97	63.92	61.20	78.41	63.70	72.58	79.09	73.96	92.93
2	3.95	5.98	9.81	13.86	21.90	24.91	33.02	35.64	46.46	53.31	60.30	69.98	76.80	84.67	93.10	97.34	117.74	108.00	148.10	132.30	124.42	152.10	141.20	162.62
3	1.96	4.90	4.91	20.63	11.00	37.58	16.64	56.70	23.23	25.87	92.70	114.05	38.40	128.77	48.67	45.97	63.92	194.40	217.80	63.70	217.73	243.36	73.96	92.93
4	4.95	5.98	20.05	13.86	21.90	51.26	67.84	35.64	46.46	112.90	60.30	138.67	155.20	84.67	93.10	200.10	117.74	234.00	148.10	132.30	254.02	152.10	141.20	348.48
5	1.96	2.94	8.83	6.88	54.50	12.24	16.64	16.20	23.23	25.87	158.40	36.29	198.40	42.34	48.67	45.97	63.92	298.80	78.41	338.10	72.58	79.09	73.96	92.93
6	3.95	9.97	9.81	41.76	21.90	75.89	33.02	113.08	46.46	53.31	184.50	213.84	76.80	250.49	93.10	97.34	117.74	352.80	413.82	132.30	409.54	474.55	141.20	162.62
7	1.96	2.94	4.91	12.82	11.00	12.24	16.64	16.20	23.23	202.27	27.90	36.29	38.40	292.82	48.67	45.97	63.92	61.20	78.41	480.20	72.58	79.09	73.96	92.93
8	5.95	5.98	20.05	13.86	21.90	51.26	133.89	35.64	46.46	112.90	60.30	138.67	320.00	84.67	93.10	200.10	117.74	234.00	148.10	132.30	533.95	152.10	141.20	627.26
9	1.96	6.86	4.91	20.63	11.00	37.58	16.64	166.21	23.23	25.87	92.70	339.55	38.40	128.77	48.67	45.97	63.92	194.40	217.80	63.70	616.90	243.36	73.96	92.93
10	3.95	5.98	17.66	13.86	109.00	24.91	33.02	35.64	46.46	53.31	312.30	69.98	404.80	84.67	93.10	97.34	117.74	597.60	148.10	676.20	124.42	152.10	141.20	162.62
11	1.96	2.94	4.91	6.88	21.10	12.24	16.64	16.20	246.84	25.87	27.90	36.29	38.40	42.34	48.67	45.97	63.92	61.20	766.66	63.70	72.58	79.09	73.96	998.98
12	4.95	9.97	20.05	41.76	21.90	155.52	67.84	113.08	46.46	112.90	184.50	432.86	155.20	250.49	93.10	200.10	117.74	727.20	413.82	132.30	844.99	474.55	141.20	348.48

N=2000	Count of occurences of primefactor p in the (partial) Eulerproduct over prime(1)...prime(2000)
s\p	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73	79	83	89
1	3965	1479	617	384	221	183	132	107	91	75	62	55	50	47	46	34	36	35	31	29	28	27	26	21
2	7979	2986	1226	777	440	359	259	233	184	146	129	112	97	97	86	73	67	65	55	60	53	51	47	43
3	3965	2469	617	1154	221	541	132	347	91	75	205	170	50	152	46	34	36	106	90	29	85	82	26	21
4	9978	2986	2494	777	440	721	522	233	184	296	129	230	199	97	86	152	67	134	55	60	105	51	47	90
5	3965	1479	1112	384	1102	183	132	107	91	75	332	55	244	47	46	34	36	162	31	143	28	27	26	21
6	7979	4985	1226	2333	440	1072	259	711	184	146	406	340	97	298	86	73	67	201	174	60	168	165	47	43
7	3965	1479	617	716	221	183	132	107	91	505	62	55	50	338	46	34	36	35	31	199	28	27	26	21
8	11977	2986	2494	777	440	721	1059	233	184	296	129	230	403	97	86	152	67	134	55	60	212	51	47	179
9	3965	3459	617	1154	221	541	132	1034	91	75	205	503	50	152	46	34	36	106	90	29	252	82	26	21
10	7979	2986	2210	777	2195	359	259	233	184	146	673	112	504	97	86	73	67	330	55	284	53	51	47	43
11	3965	1479	617	384	420	183	132	107	1040	75	62	55	50	47	46	34	36	35	340	29	28	27	26	250
12	9978	4985	2494	2333	440	2166	522	711	184	296	406	685	199	298	86	152	67	408	174	60	334	165	47	90
	relative frequency: count/N*(p_k - 1)²
1	1.98	2.96	4.94	6.91	11.05	13.18	16.90	17.33	22.02	29.40	27.90	35.64	40.00	41.45	48.67	45.97	60.55	63.00	67.52	71.05	72.58	82.13	87.41	81.31
2	3.99	5.97	9.81	13.99	22.00	25.85	33.15	37.75	44.53	57.23	58.05	72.58	77.60	85.55	90.99	98.70	112.69	117.00	119.79	147.00	137.38	155.14	158.01	166.50
3	1.98	4.94	4.94	20.77	11.05	38.95	16.90	56.21	22.02	29.40	92.25	110.16	40.00	134.06	48.67	45.97	60.55	190.80	196.02	71.05	220.32	249.44	87.41	81.31
4	4.99	5.97	19.95	13.99	22.00	51.91	66.82	37.75	44.53	116.03	58.05	149.04	159.20	85.55	90.99	205.50	112.69	241.20	119.79	147.00	272.16	155.14	158.01	348.48
5	1.98	2.96	8.90	6.91	55.10	13.18	16.90	17.33	22.02	29.40	149.40	35.64	195.20	41.45	48.67	45.97	60.55	291.60	67.52	350.35	72.58	82.13	87.41	81.31
6	3.99	9.97	9.81	41.99	22.00	77.18	33.15	115.18	44.53	57.23	182.70	220.32	77.60	262.84	90.99	98.70	112.69	361.80	378.97	147.00	435.46	501.93	158.01	166.50
7	1.98	2.96	4.94	12.89	11.05	13.18	16.90	17.33	22.02	197.96	27.90	35.64	40.00	298.12	48.67	45.97	60.55	63.00	67.52	487.55	72.58	82.13	87.41	81.31
8	5.99	5.97	19.95	13.99	22.00	51.91	135.55	37.75	44.53	116.03	58.05	149.04	322.40	85.55	90.99	205.50	112.69	241.20	119.79	147.00	549.50	155.14	158.01	693.09
9	1.98	6.92	4.94	20.77	11.05	38.95	16.90	167.51	22.02	29.40	92.25	325.94	40.00	134.06	48.67	45.97	60.55	190.80	196.02	71.05	653.18	249.44	87.41	81.31
10	3.99	5.97	17.68	13.99	109.75	25.85	33.15	37.75	44.53	57.23	302.85	72.58	403.20	85.55	90.99	98.70	112.69	594.00	119.79	695.80	137.38	155.14	158.01	166.50
11	1.98	2.96	4.94	6.91	21.00	13.18	16.90	17.33	251.68	29.40	27.90	35.64	40.00	41.45	48.67	45.97	60.55	63.00	740.52	71.05	72.58	82.13	87.41	968.00
12	4.99	9.97	19.95	41.99	22.00	155.95	66.82	115.18	44.53	116.03	182.70	443.88	159.20	262.84	90.99	205.50	112.69	734.40	378.97	147.00	865.73	501.93	158.01	348.48

N=10000	Count of occurences of primefactor p in the (partial) Eulerproduct over prime(1)...prime(10000)
s\p	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73	79	83	89
1	19954	7498	3110	1922	1086	898	660	574	464	369	348	280	257	251	219	193	179	172	150	153	138	134	115	106
2	39960	14984	6211	3857	2202	1789	1322	1169	941	738	688	567	515	489	444	385	347	346	294	293	279	257	238	221
3	19954	12486	3110	5783	1086	2702	660	1750	464	369	1047	863	257	739	219	193	179	516	458	153	423	390	115	106
4	49959	14984	12495	3857	2202	3586	2640	1169	941	1489	688	1137	1024	489	444	784	347	678	294	293	561	257	238	442
5	19954	7498	5594	1922	5487	898	660	574	464	369	1737	280	1257	251	219	193	179	835	150	737	138	134	115	106
6	39960	24983	6211	11642	2202	5408	1322	3520	941	738	2080	1714	515	1443	444	385	347	1030	915	293	848	774	238	221
7	19954	7498	3110	3583	1086	898	660	574	464	2566	348	280	257	1712	219	193	179	172	150	1006	138	134	115	106
8	59958	14984	12495	3857	2202	3586	5297	1169	941	1489	688	1137	2045	489	444	784	347	678	294	293	1130	257	238	899
9	19954	17474	3110	5783	1086	2702	660	5274	464	369	1047	2554	257	739	219	193	179	516	458	153	1268	390	115	106
10	39960	14984	11186	3857	11007	1789	1322	1169	941	738	3443	567	2561	489	444	385	347	1689	294	1442	279	257	238	221
11	19954	7498	3110	1922	2076	898	660	574	5204	369	348	280	257	251	219	193	179	172	1680	153	138	134	115	1245
12	49959	24983	12495	11642	2202	10840	2640	3520	941	1489	2080	3434	1024	1443	444	784	347	2041	915	293	1700	774	238	442
	relative frequency rounded to integer: count/N*(p_k - 1)²
1	2	3	5	7	11	13	17	19	22	29	31	36	41	44	46	52	60	62	65	75	72	82	77	82
2	4	6	10	14	22	26	34	38	46	58	62	73	82	86	94	104	117	125	128	144	145	156	160	171
3	2	5	5	21	11	39	17	57	22	29	94	112	41	130	46	52	60	186	200	75	219	237	77	82
4	5	6	20	14	22	52	68	38	46	117	62	147	164	86	94	212	117	244	128	144	291	156	160	342
5	2	3	9	7	55	13	17	19	22	29	156	36	201	44	46	52	60	301	65	361	72	82	77	82
6	4	10	10	42	22	78	34	114	46	58	187	222	82	255	94	104	117	371	399	144	440	471	160	171
7	2	3	5	13	11	13	17	19	22	201	31	36	41	302	46	52	60	62	65	493	72	82	77	82
8	6	6	20	14	22	52	136	38	46	117	62	147	327	86	94	212	117	244	128	144	586	156	160	696
9	2	7	5	21	11	39	17	171	22	29	94	331	41	130	46	52	60	186	200	75	657	237	77	82
10	4	6	18	14	110	26	34	38	46	58	310	73	410	86	94	104	117	608	128	707	145	156	160	171
11	2	3	5	7	21	13	17	19	252	29	31	36	41	44	46	52	60	62	732	75	72	82	77	964
12	5	10	20	42	22	156	68	114	46	117	187	445	164	255	94	212	117	735	399	144	881	471	160	342

N=20000	Count of occurences of primefactor p in the (partial) Eulerproduct over prime(1)...prime(20000)
s\p	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73	79	83	89
1	40152	15083	6247	3897	2195	1812	1332	1170	946	742	683	574	524	489	444	394	357	336	307	294	282	273	236	231
2	80415	30152	12538	7804	4393	3613	2665	2351	1902	1481	1380	1147	1042	984	898	786	711	691	614	578	555	528	491	475
3	40152	25127	6247	11690	2195	5402	1332	3552	946	742	2063	1724	524	1511	444	394	357	1012	917	294	841	779	236	231
4	100537	30152	25157	7804	4393	7249	5351	2351	1902	2978	1380	2289	2074	984	898	1581	711	1376	614	578	1132	528	491	929
5	40152	15083	11256	3897	11040	1812	1332	1170	946	742	3454	574	2544	489	444	394	357	1707	307	1459	282	273	236	231
6	80415	50274	12538	23461	4393	10852	2665	7069	1902	1481	4169	3440	1042	2965	898	786	711	2043	1856	578	1671	1558	491	475
7	40152	15083	6247	7245	2195	1812	1332	1170	946	5188	683	574	524	3419	444	394	357	336	307	2005	282	273	236	231
8	120659	30152	25157	7804	4393	7249	10673	2351	1902	2978	1380	2289	4142	984	898	1581	711	1376	614	578	2257	528	491	1835
9	40152	35171	6247	11690	2195	5402	1332	10600	946	742	2063	5128	524	1511	444	394	357	1012	917	294	2574	779	236	231
10	80415	30152	22571	7804	22113	3613	2665	2351	1902	1481	6912	1147	5150	984	898	786	711	3423	614	2903	555	528	491	475
11	40152	15083	6247	3897	4201	1812	1332	1170	10477	742	683	574	524	489	444	394	357	336	3378	294	282	273	236	2541
12	100537	50274	25157	23461	4393	21787	5351	7069	1902	2978	4169	6928	2074	2965	898	1581	711	4077	1856	578	3374	1558	491	929
	relative frequency rounded to integer: count/N*(p_k - 1)²
1	2	3	5	7	11	13	17	19	23	29	31	37	42	43	47	53	60	60	67	72	73	83	79	89
2	4	6	10	14	22	26	34	38	46	58	62	74	83	87	95	106	120	124	134	142	144	161	165	184
3	2	5	5	21	11	39	17	58	23	29	93	112	42	133	47	53	60	182	200	72	218	237	79	89	p=1(mod3)
4	5	6	20	14	22	52	68	38	46	117	62	148	166	87	95	214	120	248	134	142	293	161	165	360
5	2	3	9	7	55	13	17	19	23	29	155	37	204	43	47	53	60	307	67	357	73	83	79	89	p=1(mod5)
6	4	10	10	42	22	78	34	115	46	58	188	223	83	262	95	106	120	368	404	142	433	474	165	184
7	2	3	5	13	11	13	17	19	23	203	31	37	42	302	47	53	60	60	67	491	73	83	79	89	p=1(mod7)
8	6	6	20	14	22	52	137	38	46	117	62	148	331	87	95	214	120	248	134	142	585	161	165	711
9	2	7	5	21	11	39	17	172	23	29	93	332	42	133	47	53	60	182	200	72	667	237	79	89
10	4	6	18	14	111	26	34	38	46	58	311	74	412	87	95	106	120	616	134	711	144	161	165	184
11	2	3	5	7	21	13	17	19	254	29	31	37	42	43	47	53	60	60	736	72	73	83	79	984
12	5	10	20	42	22	157	68	115	46	117	188	449	166	262	95	214	120	734	404	142	875	474	165	360

N=41000	Count of occurences of primefactor p in the (partial) Eulerproduct over prime(1)...prime(41000)
s\p	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73	79	83	89
1	81841	30680	12814	7923	4478	3702	2716	2385	1936	1527	1382	1167	1061	990	919	797	724	692	633	593	561	541	497	466
2	163877	61441	25591	15930	9021	7381	5426	4826	3879	3016	2804	2332	2112	1980	1838	1598	1445	1401	1258	1184	1123	1058	1017	936
3	81841	51149	12814	23840	4478	11087	2716	7196	1936	1527	4205	3503	1061	3025	919	797	724	2095	1897	593	1700	1591	497	466
4	204876	61441	51242	15930	9021	14805	10898	4826	3879	6024	2804	4664	4216	1980	1838	3204	1445	2797	1258	1184	2277	1058	1017	1874
5	81841	30680	23065	7923	22438	3702	2716	2385	1936	1527	7021	1167	5228	990	919	797	724	3468	633	2972	561	541	497	466
6	163877	102440	25591	47837	9021	22149	5426	14425	3879	3016	8478	7014	2112	5992	1838	1598	1445	4175	3786	1184	3421	3171	1017	936
7	81841	30680	12814	14732	4478	3702	2716	2385	1936	10626	1382	1167	1061	6987	919	797	724	692	633	4139	561	541	497	466
8	245875	61441	51242	15930	9021	14805	21766	4826	3879	6024	2804	4664	8412	1980	1838	3204	1445	2797	1258	1184	4560	1058	1017	3738
9	81841	71618	12814	23840	4478	11087	2716	21571	1936	1527	4205	10482	1061	3025	919	797	724	2095	1897	593	5181	1591	497	466
10	163877	61441	46070	15930	45072	7381	5426	4826	3879	3016	14094	2332	10496	1980	1838	1598	1445	6934	1258	5930	1123	1058	1017	936
11	81841	30680	12814	7923	8572	3702	2716	2385	21357	1527	1382	1167	1061	990	919	797	724	692	6881	593	561	541	497	5145
12	204876	102440	51242	47837	9021	44365	10898	14425	3879	6024	8478	14052	4216	5992	1838	3204	1445	8356	3786	1184	6896	3171	1017	1874
	relative frequency rounded to integer: count/N*(p_k - 1)²
1	2	3	5	7	11	13	17	19	23	29	30	37	41	43	47	53	59	61	67	71	71	80	82	88
2	4	6	10	14	22	26	34	38	46	58	62	74	82	85	95	105	119	123	134	142	142	157	167	177
3	2	5	5	21	11	39	17	57	23	29	92	111	41	130	47	53	59	184	202	71	215	236	82	88	p=1(mod3)
4	5	6	20	14	22	52	68	38	46	115	62	147	165	85	95	211	119	246	134	142	288	157	167	354
5	2	3	9	7	55	13	17	19	23	29	154	37	204	43	47	53	59	305	67	355	71	80	82	88	p=1(mod5)
6	4	10	10	42	22	78	34	114	46	58	186	222	82	258	95	105	119	367	402	142	433	471	167	177
7	2	3	5	13	11	13	17	19	23	203	30	37	41	301	47	53	59	61	67	495	71	80	82	88	p=1(mod7)
8	6	6	20	14	22	52	136	38	46	115	62	147	328	85	95	211	119	246	134	142	577	157	167	706
9	2	7	5	21	11	39	17	170	23	29	92	331	41	130	47	53	59	184	202	71	655	236	82	88
10	4	6	18	14	110	26	34	38	46	58	309	74	410	85	95	105	119	609	134	709	142	157	167	177
11	2	3	5	7	21	13	17	19	252	29	30	37	41	43	47	53	59	61	731	71	71	80	82	972
12	5	10	20	42	22	156	68	114	46	115	186	444	165	258	95	211	119	734	402	142	872	471	167	354