Tetration Gottfried Helms - Univ Kassel 01 - 2008

Continuous U_e-Tetration (f(x) = exp(x)-1, iterated)

Radius of convergence is zero for fractional heights h

In their article "On analytic iteration" Erdös & Jabotinsky [1] stated 1960, that "the function e^z-1 was shown by I.N.Baker to have no real non-integer iterates" and cited I.N.Bakers article of 1958.

However, I.N.Baker [2] deals with this question in terms of "radius of convergence", and the focus of his proof is, that "the radius of convergence isnonzero iff the iterator h is integer" (rough translation).

The latter can be shown by numerical examples. However, although the simple inspection seconds this strongly, the zero-radius of convergence does not mean, that to such a powerseries a value could not be assigned principally. If we study powerseries in the well established context of summation of divergent series (see for instance [3] or [4]), we are no more lost in space: we may apply Cesaro-/Euler- or Borel-summation to assign values to a divergent series, if their terms oscillate in sign and "diverge not too strong" (L. Euler).

Thus, if we can show, that the growthrate of the terms of the occuring series "is not too strong", then we may assign values to continuous U-tetration as well, based on those concepts of divergent summation.

From empirical evidence it seems, that the growthrate of terms is roughly hypergeometric (the logarithms of their absolute values increase roughly with their index) and may be Euler- or Borel-summable.

Adding the concept of divergent summation seems to fill the gap, which is the reason for the common expression, that continuous iteration / tetration were not existent/meaningful.

Update 8.12.2010: tables 2 and 3 were wrong; graphical plots added

---

Table 1) Terms of powerseries for U-tetration f°¹(x) = exp(x)-1, for different "height" h

The powerseries for f°^h(x) is constructed, if the terms of one column are associated with a power of x, so

f°¹(x) = 0 + 1.0*x + 0.5*x² + 0.1666*x³ + 0.041666*x⁴ + ...

h=1	h=1+1e-10	h=1+1e-9	h=1+1e-8	h=1+1e-7	h=1.000001	h=1.00001	h=1.0001	h=1.001	h=1.01	h=1.1
0	0	0	0	0	0	0	0	0	0	0
1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000	1.00000000000
0.500000000000	0.500000000050	0.500000000500	0.500000005000	0.500000050000	0.500000500000	0.500005000000	0.500050000000	0.500500000000	0.505000000000	0.550000000000
0.166666666667	0.166666666708	0.166666667083	0.166666670833	0.166666708333	0.166667083334	0.166670833358	0.166708335833	0.167083583333	0.170858333333	0.210833333333
0.0416666666667	0.0416666666854	0.0416666668542	0.0416666685417	0.0416666854167	0.0416668541669	0.0416685416938	0.0416854193751	0.0418544376250	0.0435688750000	0.0632500000000
0.00833333333333	0.00833333333903	0.00833333339028	0.00833333390278	0.00833333902778	0.00833339027792	0.00833390279236	0.00833902923627	0.00839042377090	0.00891752145833	0.0156520833333
0.00138888888889	0.00138888889020	0.00138888890197	0.00138888901968	0.00138889019676	0.00138890196764	0.00138901968094	0.00139019726109	0.00140201786294	0.00152479082778	0.00330439236111
0.000198412698413	0.000198412698664	0.000198412700926	0.000198412723545	0.000198412949736	0.000198415211653	0.000198437831961	0.000198664148515	0.000200938693519	0.000224854764284	0.000619448412698
0.0000248015873016	0.0000248015873400	0.0000248015876860	0.0000248015911458	0.0000248016257441	0.0000248019717289	0.0000248054318209	0.0000248400570949	0.0000251887541028	0.0000289291637162	0.000103086328125
0.00000275573192240	0.00000275573192619	0.00000275573196029	0.00000275573230131	0.00000275573571153	0.00000275576981414	0.00000275611087794	0.00000275952529651	0.00000279404961159	0.00000317944735419	0.0000139371209491
0.000000275573192240	0.000000275573193772	0.000000275573207557	0.000000275573345413	0.000000275574723968	0.000000275588509546	0.000000275726367947	0.000000277105214294	0.000000290920211150	0.000000432038819637	0.00000265797691816
0.0000000250521083854	0.0000000250521086406	0.0000000250521109366	0.0000000250521338968	0.0000000250523634998	0.0000000250546595623	0.0000000250776234941	0.0000000253075935284	0.0000000276403744666	0.0000000542870818543	0.000000694792899125
0.00000000208767569879	0.00000000208767508886	0.00000000208766959950	0.00000000208761470595	0.00000000208706577045	0.00000000208157641849	0.00000000202668320538	0.00000000147778177866	-0.00000000400810172166	-0.0000000584935612695	-0.000000504664368756
1.60590438368E-10	1.60590634904E-10	1.60592403728E-10	1.60610091959E-10	1.60786974092E-10	1.62555776881E-10	1.80241951284E-10	0.000000000356918343734	0.00000000210514446846	0.0000000177318932836	-0.00000000421802807312
1.14707455977E-11	1.14711315701E-11	1.14746053210E-11	1.15093428309E-11	1.18567180149E-11	1.53304783117E-11	5.00689269706E-11	0.000000000397537943013	0.00000000388064141333	0.0000000395131940522	0.000000435582178182
7.64716373182E-13	7.64343573715E-13	7.60988378525E-13	7.27436427861E-13	3.91917044815E-13	-2.96326442665E-12	-3.65138432155E-11	-0.000000000371896012790	-0.00000000371333021346	-0.0000000358639150239	-0.000000212854713628
4.77947733239E-14	4.75658969877E-14	4.55060099468E-14	2.49071380137E-14	-1.81081733747E-13	-2.24098569433E-12	-2.28415495699E-11	-2.28999588279E-10	-0.00000000230579288804	-0.0000000245673611746	-0.000000364113506315
2.81145725435E-15	3.37631562397E-15	8.46004094342E-15	5.92972934240E-14	5.67669746844E-13	5.65138714248E-12	5.64878471972E-11	0.000000000564781012687	0.00000000564052431814	0.0000000556347296302	0.000000440314777474
1.56192069686E-16	2.10871750162E-16	7.02988899063E-16	5.62416282482E-15	5.48361457572E-14	5.46980342549E-13	5.47085904392E-12	5.49533060394E-11	0.000000000574130308854	0.00000000818667698740	0.000000302531826895
8.22063524662E-18	-9.08613397676E-16	-9.16011969464E-15	-9.16751827296E-14	-9.16825819610E-13	-9.16833284145E-12	-9.16834682882E-11	-0.000000000916841270162	-0.00000000916898862257	-0.0000000916721406804	-0.000000842960622434
4.11031762331E-19	3.17546572127E-16	3.17176639274E-15	3.17139603745E-14	3.17135477755E-13	3.17130840788E-12	3.17088133269E-11	0.000000000316661410455	0.00000000312392851086	0.0000000269588495460	-0.000000152576230905
1.95729410634E-20	1.68192462253E-15	1.68190700898E-14	1.68190526843E-13	1.68190530239E-12	1.68190738594E-11	1.68192839437E-10	0.00000000168213835683	0.0000000168422404977	0.000000170368161242	0.00000175588878735
8.89679139245E-22	-1.44006757299E-15	-1.44006836535E-14	-1.44006836200E-13	-1.44006753577E-12	-1.44005919420E-11	-1.43997576963E-10	-0.00000000143914142805	-0.0000000143078854015	-0.000000134634795548	-0.000000447507575851
3.86817017063E-23	-3.49777585220E-15	-3.49777589582E-14	-3.49777598736E-13	-3.49777686828E-12	-3.49778567395E-11	-0.000000000349787372745	-0.00000000349875397329	-0.0000000350752749065	-0.000000359233754730	-0.00000412470467839
1.61173757110E-24	5.38854766141E-15	5.38854764161E-14	5.38854745801E-13	5.38854562339E-12	5.38852727729E-11	0.000000000538834381251	0.00000000538650878326	0.0000000536812042036	0.000000518050812288	0.00000301683343116
6.44695028438E-26	8.08723815709E-15	8.08723819079E-14	8.08723852840E-13	8.08724190448E-12	8.08727566529E-11	0.000000000808761326671	0.00000000809098861218	0.0000000812467507604	0.000000845471578850	0.0000109668435898
2.47959626322E-27	-2.08610643846E-14	-2.08610643403E-13	-2.08610638979E-12	-2.08610594741E-11	-2.08610152358E-10	-0.00000000208605728378	-0.0000000208561473527	-0.000000208117422036	-0.00000203528517695	-0.0000145013111830
9.18368986380E-29	-1.98804698507E-14	-1.98804699874E-13	-1.98804713544E-12	-1.98804850238E-11	-1.98806217180E-10	-0.00000000198819886437	-0.0000000198956562364	-0.000000200321652762	-0.00000213800535957	-0.0000326762521589
3.27988923707E-30	8.81620790832E-14	8.81620789730E-13	8.81620778708E-12	8.81620668487E-11	0.000000000881619566273	0.00000000881608543492	0.0000000881498251899	0.000000880388962326	0.00000868663597280	0.0000694414439273
1.13099628864E-31	4.63981159513E-14	4.63981165588E-13	4.63981226334E-12	4.63981833790E-11	0.000000000463987908352	0.00000000464048653567	0.0000000464656064883	0.000000470726072383	0.00000530992672531	0.000106885408600
3.76998762882E-33	-4.13467904020E-13	-4.13467903782E-12	-4.13467901408E-11	-0.000000000413467877659	-0.00000000413467640175	-0.0000000413465265028	-0.000000413441483749	-0.00000413200690203	-0.0000410495847765	-0.000355577741558
1.21612504155E-34	-5.66858222391E-14	-5.66858252371E-13	-5.66858552172E-12	-5.66861550181E-11	-0.000000000566891530263	-0.00000000567191330385	-0.0000000570189261868	-0.000000600161489809	-0.00000899062056549	-0.000369687954408
3.80039075485E-36	2.16041905589E-12	2.16041905589E-11	2.16041905593E-10	0.00000000216041905629	0.0000000216041905989	0.000000216041909431	0.00000216041928365	0.0000216040568546	0.000215872174746	0.00199175357147
1.15163356208E-37	-5.47077213909E-13	-5.47077197440E-12	-5.47077032756E-11	-0.000000000547075385908	-0.00000000547058917425	-0.0000000546894232342	-0.000000545247356215	-0.00000528776126910	-0.0000363878979814	0.00124233837477
3.38715753552E-39	-1.25626433413E-11	-1.25626433480E-10	-0.00000000125626434144	-0.0000000125626440785	-0.000000125626507196	-0.00000125627171216	-0.0000125633802464	-0.000125699219759	-0.00126263688985	-0.0122956957964
9.67759295863E-41	8.40257859633E-12	8.40257849583E-11	0.000000000840257749086	0.00000000840256744117	0.0000000840246694420	0.000000840146196927	0.00000839141170106	0.0000829085750100	0.000728054068510	-0.00291910126219
2.68822026629E-42	8.10158740611E-11	0.000000000810158741453	0.00000000810158749874	0.0000000810158834080	0.000000810159676138	0.00000810168096143	0.0000810252238860	0.000811087929800	0.00818868469497	0.0837613814163
7.26546017915E-44	-9.15286631426E-11	-0.000000000915286624639	-0.00000000915286556770	-0.0000000915285878083	-0.000000915279091204	-0.00000915211221816	-0.0000914532468473	-0.000907739013235	-0.00839237669014	-0.0123753895818
1.91196320504E-45	-0.000000000576761196551	-0.00000000576761197451	-0.0000000576761206446	-0.000000576761296404	-0.00000576762195971	-0.0000576771191244	-0.000576861103416	-0.00577756166342	-0.0586297852900	-0.628707423372
4.90246975651E-47	0.000000000955571716719	0.00000000955571711672	0.0000000955571661193	0.000000955571156410	0.00000955566108576	0.0000955515629597	0.000955010776668	0.00949955952176	0.0898797024579	0.346005170544
1.22561743913E-48	0.00000000450869740944	0.0000000450869741897	0.000000450869751430	0.00000450869846761	0.0000450870800063	0.000450880332773	0.00450975628349	0.0451925428938	0.461104613865	5.18460562367
2.98931082714E-50	-0.0000000102595421705	-0.000000102595421294	-0.00000102595417181	-0.0000102595376059	-0.000102594964837	-0.00102590852542	-0.0102549722775	-0.102137744719	-0.979514574288	-5.10900840368
7.11740673129E-52	-0.0000000384760242903	-0.000000384760243955	-0.00000384760254466	-0.0000384760359579	-0.000384761410707	-0.00384771921724	-0.0384877005134	-0.385925159878	-3.96135098279	-46.8048484100
1.65521086774E-53	0.000000116227861718	0.00000116227861353	0.0000116227857706	0.000116227821235	0.00116227456523	0.0116223809326	0.116187329617	1.15821760352	11.2090207909	68.6891875853
3.76184288123E-55	0.000000356115418772	0.00000356115420001	0.0000356115432287	0.000356115555157	0.00356116783848	0.0356129070510	0.356251912476	3.57477862313	36.9486067074	460.737734874
8.35965084718E-57	-0.00000140454749128	-0.0000140454748778	-0.000140454745280	-0.00140454710305	-0.0140454360555	-0.140450862959	-1.40415877660	-14.0065092062	-136.465277745	-927.516816580
1.81731540156E-58	-0.00000354820288308	-0.0000354820289843	-0.000354820305193	-0.00354820458692	-0.0354821993676	-0.354837343270	-3.54990814732	-35.6523075915	-371.594948853	-4924.66176075
3.86662851396E-60	0.0000181898851298	0.000181898850939	0.00181898847341	0.0181898811366	0.181898451611	1.81894853944	18.1858865205	181.497772157	1777.67618340	13012.1386393
8.05547607075E-62	0.0000377112981275	0.000377112983331	0.00377113003895	0.0377113209530	0.377115265879	3.77135829113	37.7341435490	379.394895942	3996.61935891	56902.5880715
1.64397470832E-63	-0.000252879703867	-0.00252879703474	-0.0252879699546	-0.252879660257	-2.52879267376	-25.2875338389	-252.836031788	-2524.41293675	-24832.8174530	-192427.589592
3.28794941663E-65	-0.000422329790981	-0.00422329793938	-0.0422329823508	-0.422330119212	-4.22333076246	-42.2362646294	-422.658317711	-4256.12115341	-45484.8039105	-707403.008826
6.44695964046E-67	0.00377426676588	0.0377426676139	0.377426671649	3.77426626745	37.7426177707	377.421687072	3773.76755817	37692.4954417	372159.752186	3019868.06295
1.23979993086E-68	0.00489160363873	0.0489160368436	0.489160414068	4.89160870390	48.9165433606	489.211065428	4896.67349905	49422.6804194	539466.261062	9413058.26845
2.33924515256E-70	-0.0604307388101	-0.604307387576	-6.04307382329	-60.4307329855	-604.306805109	-6043.01557255	-60424.9038957	-603719.882403	-5980329.73442	-50445247.9343
4.33193546770E-72	-0.0566594041475	-0.566594049025	-5.66594124522	-56.6594879489	-566.602429160	-5666.77925473	-56743.2849198	-574978.118900	-6500075.49449	-133274607.606
7.87624630492E-74	1.03670175242	10.3670175183	103.670174584	1036.70168597	10367.0108724	103669.509927	1036635.15163	10360288.7816	102928880.951	897923432.867
1.40647255445E-75	0.606849098219	6.06849111592	60.6849245327	606.850582677	6068.63956171	60699.7690680	608334.992559	6217036.42925	75490638.2495	1993335271.96
2.46749570956E-77	-19.0269222427	-190.269222369	-1902.69221781	-19026.9215903	-190269.157127	-1902685.69243	-19026267.7956	-190202521.170	-1894768138.29	-17031649388.3
4.25430294752E-79	-4.42173613236	-44.2173638561	-442.173891809	-4421.76424289	-44220.1749090	-442454.996746	-4449874.38446	-47030827.9756	-723070354.932	-31194996106.3
7.21068296190E-81	372.982633737	3729.82633716	37298.2633506	372982.631407	3729826.10412	37298240.0214	372980273.923	3729565793.59	37247662915.3	344046161128.
1.20178049365E-82	-47.3141710721	-473.141659540	-4731.41147732	-47313.6029646	-473084.848783	-4725730.39960	-46745493.2171	-416272077.263	955549405.335	503699141092.
1.97013195680E-84	-7795.99574192	-77959.9574336	-779599.575779	-7795995.90208	-77959973.4494	-779601176.844	-7796155496.61	-77975420891.4	-780633582303.	-7.39446331771E12
3.17763218839E-86	3875.12528713	38751.2517693	387512.407492	3875113.05484	38750028.5403	387390084.361	3862880510.59	37526546856.2	264853251990.	-8.19505248641E12
5.04386061649E-88	173446.620895	1734466.20968	17344662.1695	173446628.962	1734467016.36	17344742826.3	173454683290.	1.73526108724E12	1.74127664895E13	1.68897077763E14

Table 2: log₁₀ of absolute values of terms

h=1	h=1+1e-10	h=1+1e-9	h=1+1e-8	h=1+1e-7	h=1+1e-6	h=1+1e-5	h=1+1e-4	h=1.001	h=1.01	h=1.1
0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3006	-0.2967	-0.2596
-0.7782	-0.7782	-0.7782	-0.7782	-0.7782	-0.7782	-0.7781	-0.7780	-0.7771	-0.7674	-0.6761
-1.3802	-1.3802	-1.3802	-1.3802	-1.3802	-1.3802	-1.3802	-1.3800	-1.3783	-1.3608	-1.1989
-2.0792	-2.0792	-2.0792	-2.0792	-2.0792	-2.0792	-2.0792	-2.0789	-2.0762	-2.0498	-1.8054
-2.8573	-2.8573	-2.8573	-2.8573	-2.8573	-2.8573	-2.8573	-2.8569	-2.8532	-2.8168	-2.4809
-3.7024	-3.7024	-3.7024	-3.7024	-3.7024	-3.7024	-3.7024	-3.7019	-3.6969	-3.6481	-3.2080
-4.6055	-4.6055	-4.6055	-4.6055	-4.6055	-4.6055	-4.6055	-4.6048	-4.5988	-4.5387	-3.9868
-5.5598	-5.5598	-5.5598	-5.5598	-5.5598	-5.5598	-5.5597	-5.5592	-5.5538	-5.4976	-4.8558
-6.5598	-6.5598	-6.5598	-6.5598	-6.5598	-6.5597	-6.5595	-6.5574	-6.5362	-6.3645	-5.5754
-7.6012	-7.6012	-7.6012	-7.6012	-7.6012	-7.6011	-7.6007	-7.5967	-7.5585	-7.2653	-6.1581
-8.6803	-8.6803	-8.6803	-8.6803	-8.6805	-8.6816	-8.6932	-8.8304	-8.3971	-7.2329	-6.2970
-9.7943	-9.7943	-9.7943	-9.7942	-9.7937	-9.7890	-9.7441	-9.4474	-8.6767	-7.7512	-8.3749
-10.9404	-10.9404	-10.9403	-10.9389	-10.9260	-10.8144	-10.3004	-9.4006	-8.4111	-7.4033	-6.3609
-12.1165	-12.1167	-12.1186	-12.1382	-12.4068	-11.5282	-10.4375	-9.4296	-8.4302	-7.4453	-6.6719
-13.3206	-13.3227	-13.3419	-13.6037	-12.7421	-11.6496	-10.6413	-9.6402	-8.6372	-7.6096	-6.4388
-14.5511	-14.4716	-14.0726	-13.2270	-12.2459	-11.2478	-10.2480	-9.2481	-8.2487	-7.2547	-6.3562
-15.8063	-15.6760	-15.1531	-14.2499	-13.2609	-12.2620	-11.2619	-10.2600	-9.2410	-8.0869	-6.5192
-17.0851	-15.0416	-14.0381	-13.0377	-12.0377	-11.0377	-10.0377	-9.0377	-8.0377	-7.0378	-6.0742
-18.3861	-15.4982	-14.4987	-13.4987	-12.4988	-11.4988	-10.4988	-9.4994	-8.5053	-7.5693	-6.8165
-19.7083	-14.7742	-13.7742	-12.7742	-11.7742	-10.7742	-9.7742	-8.7741	-7.7736	-6.7686	-5.7555
-21.0508	-14.8416	-13.8416	-12.8416	-11.8416	-10.8416	-9.8416	-8.8419	-7.8444	-6.8708	-6.3492
-22.4125	-14.4562	-13.4562	-12.4562	-11.4562	-10.4562	-9.4562	-8.4561	-7.4550	-6.4446	-5.3846
-23.7927	-14.2685	-13.2685	-12.2685	-11.2685	-10.2685	-9.2685	-8.2687	-7.2702	-6.2856	-5.5204
-25.1906	-14.0922	-13.0922	-12.0922	-11.0922	-10.0922	-9.0922	-8.0920	-7.0902	-6.0729	-4.9599
-26.6056	-13.6807	-12.6807	-11.6807	-10.6807	-9.6807	-8.6807	-7.6808	-6.6817	-5.6914	-4.8386
-28.0370	-13.7016	-12.7016	-11.7016	-10.7016	-9.7016	-8.7015	-7.7012	-6.6983	-5.6700	-4.4858
-29.4841	-13.0547	-12.0547	-11.0547	-10.0547	-9.0547	-8.0547	-7.0548	-6.0553	-5.0611	-4.1584
-30.9465	-13.3335	-12.3335	-11.3335	-10.3335	-9.3335	-8.3334	-7.3329	-6.3272	-5.2749	-3.9711
-32.4237	-12.3836	-11.3836	-10.3836	-9.3836	-8.3836	-7.3836	-6.3836	-5.3838	-4.3867	-3.4491
-33.9150	-13.2465	-12.2465	-11.2465	-10.2465	-9.2465	-8.2463	-7.2440	-6.2217	-5.0462	-3.4322
-35.4202	-11.6655	-10.6655	-9.6655	-8.6655	-7.6655	-6.6655	-5.6655	-4.6655	-3.6658	-2.7008
-36.9387	-12.2620	-11.2620	-10.2620	-9.2620	-8.2620	-7.2621	-6.2634	-5.2767	-4.4390	-2.9058
-38.4702	-10.9009	-9.9009	-8.9009	-7.9009	-6.9009	-5.9009	-4.9009	-3.9007	-2.8987	-1.9102
-40.0142	-11.0756	-10.0756	-9.0756	-8.0756	-7.0756	-6.0756	-5.0762	-4.0814	-3.1378	-2.5348
-41.5705	-10.0914	-9.0914	-8.0914	-7.0914	-6.0914	-5.0914	-4.0914	-3.0909	-2.0868	-1.0770
-43.1387	-10.0384	-9.0384	-8.0384	-7.0384	-6.0384	-5.0385	-4.0388	-3.0420	-2.0761	-1.9074
-44.7185	-9.2390	-8.2390	-7.2390	-6.2390	-5.2390	-4.2390	-3.2389	-2.2383	-1.2319	-0.2016
-46.3096	-9.0197	-8.0197	-7.0197	-6.0197	-5.0197	-4.0198	-3.0200	-2.0223	-1.0463	-0.4609
-47.9116	-8.3459	-7.3459	-6.3459	-5.3459	-4.3459	-3.3459	-2.3458	-1.3449	-0.3362	0.7147
-49.5244	-7.9889	-6.9889	-5.9889	-4.9889	-3.9889	-2.9889	-1.9891	-0.9908	-0.0090	0.7083
-51.1477	-7.4148	-6.4148	-5.4148	-4.4148	-3.4148	-2.4148	-1.4147	-0.4135	0.5978	1.6703
-52.7811	-6.9347	-5.9347	-4.9347	-3.9347	-2.9347	-1.9347	-0.9348	0.0638	1.0496	1.8369
-54.4246	-6.4484	-5.4484	-4.4484	-3.4484	-2.4484	-1.4484	-0.4482	0.5532	1.5676	2.6635
-56.0778	-5.8525	-4.8525	-3.8525	-2.8525	-1.8525	-0.8525	0.1474	1.1463	2.1350	2.9673
-57.7406	-5.4500	-4.4500	-3.4500	-2.4500	-1.4500	-0.4500	0.5502	1.5521	2.5701	3.6924
-59.4127	-4.7402	-3.7402	-2.7402	-1.7402	-0.7402	0.2598	1.2597	2.2589	3.2499	4.1143
-61.0939	-4.4235	-3.4235	-2.4235	-1.4235	-0.4235	0.5765	1.5767	2.5791	3.6017	4.7551
-62.7841	-3.5971	-2.5971	-1.5971	-0.5971	0.4029	1.4029	2.4028	3.4022	4.3950	5.2843
-64.4831	-3.3743	-2.3743	-1.3743	-0.3743	0.6257	1.6257	2.6260	3.6290	4.6579	5.8497
-66.1906	-2.4232	-1.4232	-0.4232	0.5768	1.5768	2.5768	3.5768	4.5763	5.5707	6.4800
-67.9066	-2.3105	-1.3105	-0.3105	0.6895	1.6895	2.6895	3.6899	4.6939	5.7320	6.9737
-69.6309	-1.2187	-0.2187	0.7813	1.7813	2.7813	3.7813	4.7812	5.7808	6.7767	7.7028
-71.3633	-1.2467	-0.2467	0.7533	1.7533	2.7533	3.7533	4.7539	5.7597	6.8129	8.1247
-73.1037	0.0157	1.0157	2.0157	3.0157	4.0157	5.0157	6.0156	7.0154	8.0125	8.9532
-74.8519	-0.2169	0.7831	1.7831	2.7831	3.7831	4.7832	5.7841	6.7936	7.8779	9.2996
-76.6077	1.2794	2.2794	3.2794	4.2794	5.2794	6.2794	7.2794	8.2792	9.2776	10.2313
-78.3712	0.6456	1.6456	2.6456	3.6456	4.6456	5.6459	6.6483	7.6724	8.8592	10.4941
-80.1420	2.5717	3.5717	4.5717	5.5717	6.5717	7.5717	8.5717	9.5717	10.5711	11.5366
-81.9202	1.6750	2.6750	3.6750	4.6750	5.6749	6.6745	7.6697	8.6194	8.9803	11.7022
-83.7055	3.8919	4.8919	5.8919	6.8919	7.8919	8.8919	9.8919	10.8920	11.8924	12.8689
-85.4979	3.5883	4.5883	5.5883	6.5883	7.5883	8.5881	9.5869	10.5743	11.4230	12.9136
-87.2972	5.2392	6.2392	7.2392	8.2392	9.2392	10.2392	11.2392	12.2394	13.2409	14.2276

The precise growthrate of terms is not yet determined. However, it seems, that the forward differences (along columns) for all documented columns tend to be roughly equal for the fractional heights, perhaps depending on some index-shift.

Table 3: forward differences 1'st order of log₁₀ of absolute values of terms

h=1	h=1+1e-10	h=1+1e-9	h=1+1e-8	h=1+1e-7	h=1+1e-6	h=1+1e-5	h=1+1e-4	h=1.001	h=1.01	h=1.1
-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3010	-0.3006	-0.2967	-0.2596
-0.4771	-0.4771	-0.4771	-0.4771	-0.4771	-0.4771	-0.4771	-0.4771	-0.4765	-0.4707	-0.4164
-0.6021	-0.6021	-0.6021	-0.6021	-0.6021	-0.6021	-0.6021	-0.6020	-0.6012	-0.5935	-0.5229
-0.6990	-0.6990	-0.6990	-0.6990	-0.6990	-0.6990	-0.6990	-0.6989	-0.6980	-0.6889	-0.6065
-0.7782	-0.7782	-0.7782	-0.7782	-0.7782	-0.7782	-0.7781	-0.7780	-0.7770	-0.7670	-0.6755
-0.8451	-0.8451	-0.8451	-0.8451	-0.8451	-0.8451	-0.8451	-0.8450	-0.8437	-0.8313	-0.7271
-0.9031	-0.9031	-0.9031	-0.9031	-0.9031	-0.9031	-0.9031	-0.9030	-0.9019	-0.8906	-0.7788
-0.9542	-0.9542	-0.9542	-0.9542	-0.9542	-0.9542	-0.9543	-0.9543	-0.9550	-0.9590	-0.8690
-1.0000	-1.0000	-1.0000	-1.0000	-1.0000	-1.0000	-0.9998	-0.9982	-0.9825	-0.8668	-0.7196
-1.0414	-1.0414	-1.0414	-1.0414	-1.0414	-1.0414	-1.0412	-1.0394	-1.0222	-0.9008	-0.5827
-1.0792	-1.0792	-1.0792	-1.0792	-1.0793	-1.0805	-1.0925	-1.2336	-0.8386	0.0324	-0.1389
-1.1139	-1.1139	-1.1139	-1.1139	-1.1133	-1.1074	-1.0509	-0.6170	-0.2797	-0.5184	-2.0779
-1.1461	-1.1461	-1.1460	-1.1447	-1.1323	-1.0254	-0.5563	0.0468	0.2656	0.3480	2.0140
-1.1761	-1.1763	-1.1784	-1.1993	-1.4808	-0.7138	-0.1371	-0.0290	-0.0191	-0.0421	-0.3110
-1.2041	-1.2060	-1.2233	-1.4655	-0.3353	-0.1213	-0.2037	-0.2106	-0.2069	-0.1643	0.2332
-1.2304	-1.1489	-0.7307	0.3767	0.4962	0.4017	0.3932	0.3920	0.3885	0.3550	0.0825
-1.2553	-1.2044	-1.0804	-1.0230	-1.0150	-1.0142	-1.0139	-1.0119	-0.9923	-0.8322	-0.1630
-1.2788	0.6344	1.1150	1.2122	1.2232	1.2243	1.2242	1.2223	1.2033	1.0491	0.4450
-1.3010	-0.4566	-0.4606	-0.4610	-0.4610	-0.4611	-0.4611	-0.4617	-0.4676	-0.5315	-0.7423
-1.3222	0.7240	0.7245	0.7246	0.7246	0.7246	0.7246	0.7253	0.7317	0.8007	1.0610
-1.3424	-0.0674	-0.0674	-0.0674	-0.0674	-0.0674	-0.0675	-0.0678	-0.0708	-0.1022	-0.5937
-1.3617	0.3854	0.3854	0.3854	0.3854	0.3854	0.3854	0.3858	0.3894	0.4262	0.9646
-1.3802	0.1877	0.1877	0.1877	0.1877	0.1877	0.1877	0.1874	0.1848	0.1590	-0.1358
-1.3979	0.1763	0.1763	0.1763	0.1763	0.1763	0.1764	0.1767	0.1800	0.2127	0.5605
-1.4150	0.4115	0.4115	0.4115	0.4115	0.4115	0.4115	0.4112	0.4085	0.3815	0.1213
-1.4314	-0.0209	-0.0209	-0.0209	-0.0209	-0.0209	-0.0209	-0.0205	-0.0166	0.0214	0.3528
-1.4472	0.6469	0.6469	0.6469	0.6469	0.6469	0.6468	0.6465	0.6429	0.6088	0.3274
-1.4624	-0.2788	-0.2788	-0.2788	-0.2788	-0.2788	-0.2787	-0.2781	-0.2719	-0.2138	0.1873
-1.4771	0.9499	0.9499	0.9499	0.9499	0.9499	0.9499	0.9493	0.9434	0.8882	0.5220
-1.4914	-0.8630	-0.8630	-0.8630	-0.8630	-0.8629	-0.8627	-0.8604	-0.8379	-0.6595	0.0169
-1.5051	1.5811	1.5811	1.5811	1.5811	1.5810	1.5808	1.5785	1.5563	1.3804	0.7314
-1.5185	-0.5965	-0.5965	-0.5965	-0.5965	-0.5965	-0.5966	-0.5979	-0.6113	-0.7732	-0.2050
-1.5315	1.3610	1.3610	1.3610	1.3610	1.3610	1.3612	1.3625	1.3761	1.5403	0.9955
-1.5441	-0.1747	-0.1747	-0.1747	-0.1747	-0.1747	-0.1747	-0.1753	-0.1807	-0.2391	-0.6245
-1.5563	0.9842	0.9842	0.9842	0.9842	0.9842	0.9842	0.9848	0.9905	1.0511	1.4578
-1.5682	0.0530	0.0530	0.0530	0.0530	0.0530	0.0529	0.0526	0.0489	0.0107	-0.8305
-1.5798	0.7994	0.7994	0.7994	0.7994	0.7994	0.7995	0.7999	0.8038	0.8442	1.7059
-1.5911	0.2193	0.2193	0.2193	0.2193	0.2193	0.2192	0.2189	0.2160	0.1855	-0.2594
-1.6021	0.6738	0.6738	0.6738	0.6738	0.6738	0.6738	0.6741	0.6774	0.7101	1.1756
-1.6128	0.3571	0.3571	0.3571	0.3571	0.3571	0.3570	0.3568	0.3541	0.3272	-0.0064
-1.6232	0.5741	0.5741	0.5741	0.5741	0.5741	0.5741	0.5744	0.5773	0.6068	0.9620
-1.6335	0.4801	0.4801	0.4801	0.4801	0.4801	0.4801	0.4798	0.4773	0.4517	0.1666
-1.6435	0.4863	0.4863	0.4863	0.4863	0.4863	0.4863	0.4866	0.4895	0.5180	0.8266
-1.6532	0.5959	0.5959	0.5959	0.5959	0.5959	0.5959	0.5957	0.5931	0.5674	0.3039
-1.6628	0.4025	0.4025	0.4025	0.4025	0.4025	0.4025	0.4028	0.4058	0.4350	0.7251
-1.6721	0.7098	0.7098	0.7098	0.7098	0.7098	0.7098	0.7095	0.7068	0.6798	0.4220
-1.6812	0.3166	0.3166	0.3166	0.3166	0.3166	0.3167	0.3170	0.3202	0.3518	0.6408
-1.6902	0.8264	0.8264	0.8264	0.8264	0.8264	0.8264	0.8261	0.8231	0.7933	0.5291
-1.6990	0.2227	0.2227	0.2227	0.2227	0.2227	0.2228	0.2232	0.2269	0.2628	0.5654
-1.7076	0.9512	0.9512	0.9512	0.9512	0.9512	0.9511	0.9508	0.9472	0.9129	0.6303
-1.7160	0.1126	0.1126	0.1126	0.1126	0.1126	0.1127	0.1131	0.1177	0.1612	0.4937
-1.7243	1.0918	1.0918	1.0918	1.0918	1.0918	1.0918	1.0913	1.0869	1.0448	0.7291
-1.7324	-0.0280	-0.0280	-0.0280	-0.0280	-0.0280	-0.0279	-0.0273	-0.0212	0.0362	0.4219
-1.7404	1.2624	1.2624	1.2624	1.2624	1.2624	1.2623	1.2617	1.2557	1.1996	0.8285
-1.7482	-0.2326	-0.2326	-0.2326	-0.2326	-0.2326	-0.2325	-0.2315	-0.2218	-0.1346	0.3463
-1.7559	1.4963	1.4963	1.4963	1.4963	1.4963	1.4962	1.4952	1.4856	1.3997	0.9317
-1.7634	-0.6338	-0.6338	-0.6338	-0.6338	-0.6337	-0.6335	-0.6310	-0.6068	-0.4184	0.2628
-1.7709	1.9261	1.9261	1.9261	1.9261	1.9261	1.9258	1.9233	1.8993	1.7119	1.0425
-1.7782	-0.8967	-0.8967	-0.8967	-0.8967	-0.8967	-0.8972	-0.9019	-0.9523	-1.5908	0.1656
-1.7853	2.2169	2.2169	2.2169	2.2169	2.2169	2.2174	2.2221	2.2726	2.9122	1.1667
-1.7924	-0.3036	-0.3036	-0.3036	-0.3036	-0.3036	-0.3037	-0.3050	-0.3176	-0.4694	0.0446
-1.7993	1.6509	1.6509	1.6509	1.6509	1.6509	1.6510	1.6523	1.6650	1.8179	1.3141

It is interesting to see the ratio of consecutive coefficients graphically.

Formal powerseries, whose consecutive coefficients approach a constant ratio have a finite radius of convergence. Formal powerseries, whose radius of convergence is infinite must have a hypergeometric rate of decrease, as for instance the formal powerseries for exp(x). Then there are formal powerseries whose ratio increases with the index, for instance the Eulerian powerseries 1!x – 2!x^2+3!x^3-… Such formal powerseries have convergence-radius zero.

As I.N. Baker has shown, all fractional iterates of f(x)=exp(x)-1 have convergence-radius zero. But they show an interesting pattern of the increase of the ratio of concecutive oefficients. In the following plot I show the log₁₀ of the ratios (actually of the absoulute value) in a double-logarithmic scale.

The blue line represents the f^°1(x) at the integer height 1; the magenta line that of f^°1+µ(x), with µ=10^-10 which means a very near-integer-iterate.

The blue line decreases linearly with the index k, which reflects, that the ratio r(k) of two coefficients of the powerseries for exp(x)-1 at the index k is just (k-1)!/k! = 1/k and thus the represented function is entire. The same ratios in the fractional iterate follow that of the integer iterate, but then begin to deviate and show oscillating behaviour. Additionally, that oscillation is also overlaid by an increase which seems to be linear in this scale.

If we look at a fractional iterate farther away from the integer-iterate we get the next plot, where now the green line indicates f^°1+µ(x) where µ=10^-1. We get the same pattern, only that the point of deviation and the beginning of oscillation is at an earlier index.

This suggests another, surprising, interpretation of the exponential-series itself: the powerseries of integer-iterates are only limits, where the index of beginning of increase is shifted to infinity – and thus does no more appear…

---

For a computation of f^°0.5(x) see the example at [6], where I computed the series using Euler-summation of order 2.5.

Additional remark:

If f(x) = exp(x) –1 is generalized to arbitrary bases f_b(x) = b^x-1, the terms of the powerseries for exp(x)-1 must be scaled by powers of u=log(b). If u<>1 (or is left symbolically) an eigensystem-decomposition of the associated triangular matrix U_b can be performed and the diagonal (and eigenvalues) are the powers of u. An arbitrary height h of iteration can then be determined by substituting u by the h'th power of u in the set of eigenvalues. Then the fractional power of U_b^h can be symbolically described and in its second column we have the coefficients for the associated powerseries for the continuous iterated f_b°^h(x).

Here are the first four terms of the powerseries of height h computed via the symbolic eigensystem-decomposition of the U-tetration-matrix S2_b (see other articles in tetration-index [5])

f_b°^h (x) = u^h * x /1!
+ u^h u (u^h-1)/(u-1) *x² /2!
+ u^h u²(u^h-1)/(u-1)* [(u^h-1)(u+1)+(u^h-u)]/(u²-1) * x³/3!
+ ...

We see, that, if u=1 , which is the case when f_b(x) = exp(x)-1, the coefficients at x have zeros in the denominator, and produce a singularity, if not u^h is a positive integer power of u and numerators cancel the denominators. By shift of the parameter x this is convertible to the usual-tetration with base eta=e^(1/e) and answers then the same question for this version of tetration.

Thus the eigensystem-decomposition may be a good approach to go to study the general question of integer vs fractional iteration in more detail.

Gottfried Helms, 5.1.2008

---

References

[1] Erdös, Paul , Jabotinsky, Eri; On analytic iteration , J. Anal. Math. 8, 361-376 (1961) (also online at digicenter göttingen)

[2] Baker, I.N.; Zusammensetzung ganzer Funktionen, Math Zeitschr. Bd. 69 pp 121-163 (1958) (also online at digicenter göttingen)

[3] Knopp, Konrad; Theorie und Anwendung unendlicher Reihen, Springer, 1964 (also online at digicenter göttingen)

[4] Hardy, G. H.; Divergent Series; New York: Oxford University Press, 1949

---

[5] Helms:Tetration-Index http://go.helms-net.de/math/tetdocs/index

[6] Helms:U-tetration, h=1/2 http://go.helms-net.de/math/tetdocs/CoefficientsForUTetration.htm

---

Snippets

[1] Erdös/Jabotinsky Pg 362

---

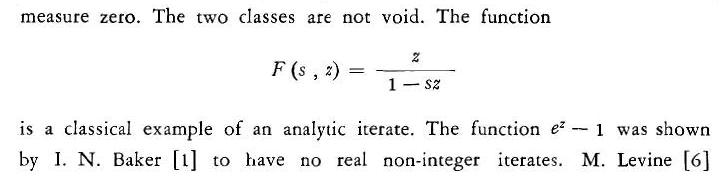
[1] Erdös/Jabotinsky Pg 376

---

[2] Baker Pg 161

---

Gottfried Helms, 8.12.2010, first version: 05.01.2008