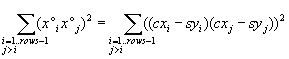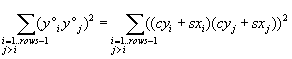|
Exercises in factor analysis
Gottfried Helms D-Kassel 2010- |
|
||||||
|
intro |
|
|
|
|
|
||
Minres by rotation
Definitions
Notation for entries of loadingsmatrix L
|
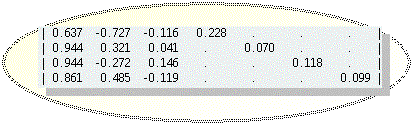
x1 y1 z1 |
L = |
x2 y2 z2 |
| x3 y3 z3 |
Here the factors are represented by the columns and the variables by the rows.
Actually this notation is only a mnemonic for the illustration of the general method of computation; the dimension for the minres-rotation is meant as arbitrary.
Method:
iteratively rotate planes (all pairs of columns/factors in one iteration) until convergence (analoguously to the jacobi-method for principal components)
Criterion for one plane-rotation:
* maximize
sum-of-squares of partial covariances ("ssp") in the left column of
the pair and
* minimize it in the right column of the pair.
Example for rotation of pair of factors X,Y
partial covariances: x1*x2 , x1*x3 , x2*x3 and y1*y2 , y1*y3 , y2*y3
ssp(X),ssp(Y)
: sums of squares of partial covariances in factors:
ssp(X)
= (x1*x2 )² + (x1*x3
)² + (x2*x3 )²
ssp(Y)
= ( y1*y2 )² + (y1*y3
)² + ( y2*y3)²
Notation for rotated X and Y:
c
= cos(φ), s = sin(φ)
X° = Xc – Ys Y° = Yc + Xs
Criterion for each rotation:
choose φ such that the sum of squared partial correlations (ssp)
|
ssp(X°)= |
|
is maximum and
|
ssp(Y°)= |
|
is minimum.
Derivation of the formula for determination of value of required φ
We can smooth the above formulae if we look for the maximum of the difference ssp(X°) – ssp(Y°). We have then
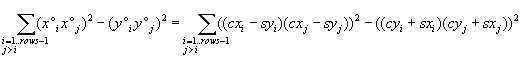
is maximum
For the inner term Ti,j for some indexes i and j we get with some rewriting:
Ti,j=![]()

|
Ti,j = |
|
Writing c2 for c²–s² = cos(φ)²–sin(φ)² = cos(2φ) and s2 for 2cs = 2cos(φ)sin(φ) = sin(2φ) we have
![]()
Reintroducing the sum over all relevant combinations of indexes i and j and separating c2 and s2 we can now write:
![]()
For convenience we reduce notation further:
![]()
and arrive at a short notation for the function of the optimization-criterion
![]()
The first derivative:
![]()
and the second derivative
![]()
A maximum occurs where
f '(φ ) = 0 f "(φ ) < 0
The formula for determination of the required rotation-angle φ :
The derivative f '(φ ) = 0
![]()
separated for the trigonometrics of the arc φ reads
![]()
or, where the expressions critx and crity are made explicite:

The arc φ (and then the required values for cos(φ) and sin(φ)) can be found by
φ
= arctan( s2/c2) /2 = arctan( –crity/critx)
/2
c = cos(φ) s = sin(φ)
But we need a bit more of discussion here because of the ambiguity of signs for s2 and c2 : -s2/-c2 lead to the same t2 as +s2/+c2 but drawn in the euclidean plane (x,y) the half angle is different for both cases. So I give a more useful derivation.
From f '(φ ) = 0 follows, that with a constant m = sqrt(critx²+crity²) we'll have with two choices for the signing of c2 and s2:
1.1)
c2 = + critx/m s2 = – crity/m
1.2) c2 = – critx/m s2 = + crity/m
from which the formula for the second derivative can be rewritten
2.1) f "(φ ) = –4(+ critx²
+ crity²)/m = –4 m
2.2) f "(φ ) = –4(– critx²
– crity²)/m = + 4 m
Since m is positive and independent of φ the choice 2.1) is required and thus from 1.1) we have now unconditionally:
c2
= critx/m
s2 = – crity/m
If we locate a vector v2 in the euclidean plane (x,y) from the origin pointing to the coordinates (c2,s2) and halve the angle 2 φ of v2 with the x-axis to get the vector v1 pointing to (c,s) we have s always positive and c negative if s2 was negative.
|
|
let the black solid vector be v2. Then the red solid vector is another solution for the criterion f'(φ )=0. However, if we halve the angle to get v1 we get significant different results (the dotted vectors with resp. color). If we have the correct vector v1, and it points into the second quadrant, we can reflect it (blue dotted vector) so that the signs of the resulting rotated factors X° and Y° do not flip around |
If we actually compute the final values cos(φ) and sin(φ) it happens, that we have a rotation φ a little less than π which reflects the signs of the x-coordinates. This is unnecessary – the sign of a complete factor can be chosen arbitrarily. If such a case occurs, we can simply invert the sign of the rotation-parameters cos(φ) and sin(φ) (or add π to the rotation angle).
Thus we have (in Pari/GP-notation)
{minres_rotplane(MAT,x,y) =
local(crit,phi,c2,s2,c1,s1,m,NEWMAT);
crit = minres_crit(MAT,x,y); \\ this
gives the vector [critx,crity]
m = sqrt( crit[1]^2 + crit[2]^2);
c2 = crit[1]/m; s2 = - crit[2]/m ;
phi
= arg2(c2 + I*s2)/2; \\ arg2
gives range 0..2*pi for phi
if(phi>Pi/2, phi+=Pi); \\ prevent flipping signs in X for small
effective rotation-angles
c1 = cos(phi); s1 = sin(phi);
NEWMAT = RotatePlane(MAT,x,y,c1,s1);
\\ this rotates two columns in a matrix given cos/sin of an angle
return(NEWMAT); }
The computation of the minres-criterion is
{minres_crit(MAT,x,y) =
local(rs=rows(M),X,Y,crit_x=0,crit_y=0,txx,tyy,txy,tyx);
X = MAT[,x]; Y = MAT[,y];
for(i=1,rs-1, for(j=i+1,rs,
txx= X[i]*X[j] ;
tyy= Y[i]*Y[j] ;
txy= X[i]*Y[j] ;
tyx= Y[i]*X[j] ;
crit_x +=
(txx+tyy)*(txx-tyy);
crit_y +=
(txx+tyy)*(txy+tyx);
));
return([crit_x,crit_y]) }
The computation of the rotation of a plane in a matrix M given the cos and sin for the rotation is
{ RotatePlane(M, x, y, rotcos, rotsin) =
local(X, Y);
X = M[,x]; Y=M[,y];
M[,x] = X*rotcos - Y*rotsin;
M[,y] = Y*rotcos + X*rotsin;
return(M); }
Gottfried Helms