Collatz-musings: 2^S/3^N - a new estimate of best approximations

Approximation 2^S to 3^N
(triggered by cycle-discussion in the Collatz-problem)
a large scale view; N = 1..10³⁸ ; a hullcurve N=1…10²⁵⁰
and some more data up to an assumed cycle length of N~10^{680 000}

1. A large-scale view into the distance of 3^N and the next perfect power of 2

1.1. The problem

In the investigation of the possibility of cycles under the Collatz-iteration (see [1]), we find, that the length N of such a hypothetic cycle and the distance of 3^N to the next greater power 2^S is a crucial relation. Here S is defined such that 2^S > 3^N and more precisely, such that

S = ceil (N log(3)/log(2) )

This relation occurs, if we express the Collatz-transformation in the "syracuse"-notation, such that

T(a) = (3a+1)/2^A on odd natural numbers a where the natural number A is such, that the result is again odd

Then N is the number of (syracuse) operations (3a_k+1)/2^Ak and S is the sum of all occuring exponents A_k.

In the standard notation

C(a)= 3a+1 (if a is odd)
C(a)= a/2 (if a is even),

the variable N indicates the number of odd operations and S is the number of a/2-operations.

If we consider the cycle, we can formulate a condition in terms of an equation which must be solvable in positive integers N,S, .

Example: assume the four consecutive elements a,b,c,d of a cyclic trajectory of N=4 steps in the syracuse-notation (it is obvious how this generalizes to arbitrary N so I just show the toy example here). Then we have that

                b = (3a+1)/2^A                 // (wlog) we assume "a" as the least element
                c = (3b+1)/2^B
                d = (3c+1)/2^C
                a = (3d+1)/2^D

If we consider the product of the lhs and of the rhs we get

bcda = (3a+1)(3b+1)(3c+1)(3d+1)/2^A+B+C+D

Writing S for the sum of exponents and reordering, we get

2^S = (3+1/a)(3+1/b)(3+1/c)(3+1/d)

We see, that the rhs becomes 4^N when a,b,c,d are all 1, the smallest allowed odd positive integer; and it approaches 3^N (from above!) if that elements all tend to infinity. Thus S must lay between ß∙N and 2∙N (where ß=log(3)/log(2)~1.59 ) and the lhs is a perfect power of 2 and must also be greater than 3^N , thus at least must be the next perfect power of 2 greater than 3^N to allow a N-step cycle. If now the elements a,b,c,d are assumed all to be larger than 1 (to describe another cycle than the trivial), then the rhs tends very fast into the near of 3^N, such that it becomes smaller than any 2^S (>3^N). For instance, for the toy-example using N=4 the rhs becomes bigger than 3⁴=81 but smaller than (3+1/5)⁴=(16/5)⁴ =104.8576 and that upper value is smaller than the next perfect power of 2 above 3^N (2⁷=128), so we know immediately that there is no 4-step-cycle possible because if we increase the assumed values for a,b,c,d to allowed values the rhs even decreases more. Here the restriction of what is "allowed" is (at least): they must be different, not divisible by 3 , and even more, but which I shall not discuss at the moment.

On the other hand, for some other N we might have the smallest 2^S above being nearer, thus some high and special N in combination with not too big members a,b,c,d,... of the assumed cycle might be possible. In the opposite direction, if we know by experimentation, that all a,b,c,... < w are not members of a cycle, where w is the empirically checked highest number then we can formulate

                if for some N and S=ceil(ß∙N)
                               2^S > (3+1/w)^N
                                               then a cycle with N elements is not possible

The critical inequality can be expressed even more concise

                               2^S /3^N > (1+1/(3w))^N
                               2^{ceil(ß∙N)-ß∙N} > (1+1/(3w))^N
                               ceil(ß∙N)-ß∙N > N∙ln(1+1/3w)/ln(2)
                               ln(2)∙(1-frac(ß∙N)) > N∙ln(1+1/(3w))
                               ln(2)∙(1-frac(ß∙N))/N > ln(1+1/(3w))

So if for some fixed w and some N under consideration

(1) ln(2)∙(1-frac(ß∙N))/N > ln(1+1/(3w))

we know, that such n N does not allow a cycle, and if

(2) ln(2)∙(1-frac(ß∙N))/N < ln(1+1/(3w))

then a cycle of that length N cannot be excluded/might exist by means of this test only.

For instance, we know that w>20∙2⁵⁸ as shown by T.Oliveira's computational verifications.

If we ask now, what is the minimal N such that (2) is satisfied,

(3) ln(2)∙(1-frac(ß∙N))/N < ln(1+1/(3w)) ~ 5.78241158659 E-20

then we can empirically check for the occurences of the smallest values in the lhs when increasing N. Based on best approximations by the convergents of the continued fractions of ß we get such a picture:

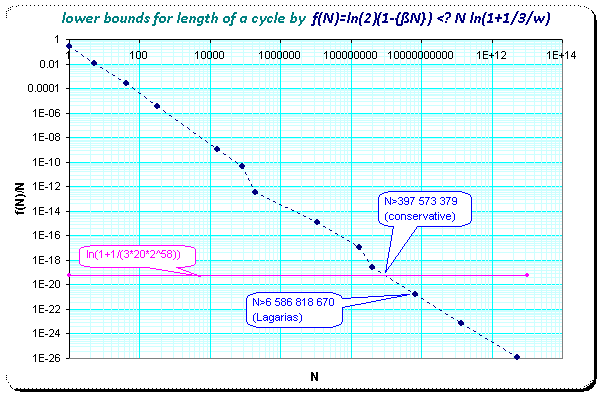
This problem motivated the consideration of the more general problem of the approximatibility of perfect powers of 3 to that of 2 for which I'll provide some data below.

1.2. The function f(N) under consideration and the hullcurve of moving minima

We write 2^S to 3^N (where N is given and S is the smallest value such that 2^S>3^N).

I produced data using the arbitrary-precision software Pari/GP.

We are interested in the relative value of that distance (2^S-3^N)/3^N =2^S/3^N-1, and use the log, because the values of the original function cannot be used with a computer if N itself goes to hundreds or thousand digits.

First we look at

                f(N)       = log(2^S/3^N)
                               = log(2)*(ceil (N ß ) – N ß)
                               = log(2)*( 1 - frac (N ß ) )

First few values for f(N) are

                log(4/3)             = log(1.333..)   ~0.287682072452 ,
                log(16/9)          = log(1.7777…)               ~ 0.575364144904
                log(32/27)                                       ~0.169899036795

(for more values see table in appendix)

The values f(N) range from 0 to log(2)~0.69314 (exclusive the bounds); a "good" approximation (small relative distance) is f(N) near zero, a "bad" approximation is f(N) near log(2). Also "better" approximations occur sporadically with increasing N, but we don't have an easy relation of N to that measure of quality of approximation. So in plot 2 I show a trend, how it appears in a larger scale view for N=1 to 10³⁸ . Then we get a much greater overview for N up to 10^{680 000} , which means, N has 680 000 digits.

1.3. First impression and the idea of a hullcurve (or envelope)

But before the plot with the trend another, more obvious plot to introduce into the idea of envelope. Here I used N=1 to N=800 and the function-values for each N.

Plot 1: Plot of approximants f(N) for some small N

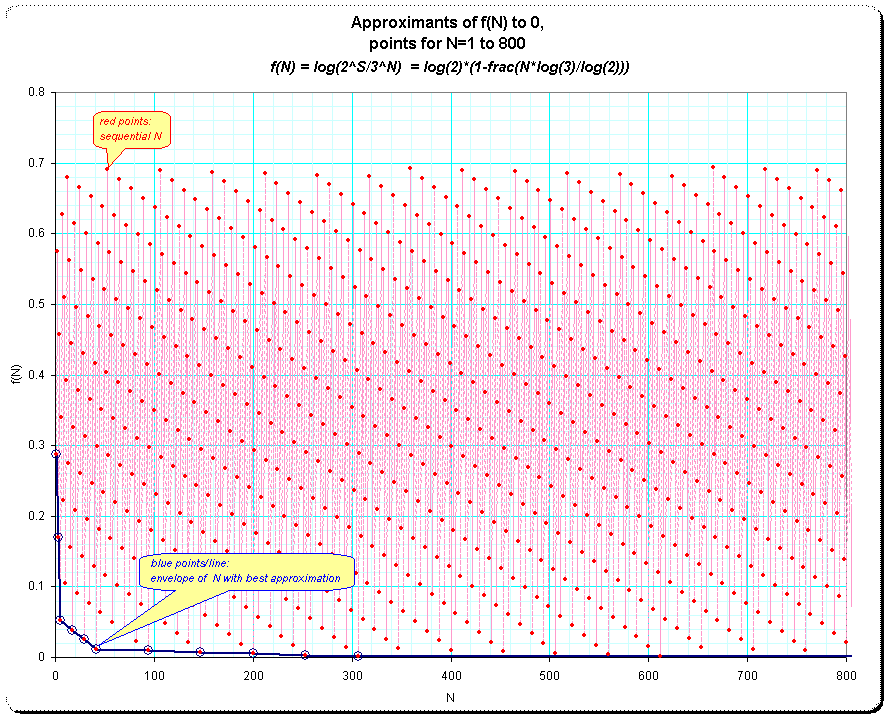
We see a clear regularity ; the apparent antidiagonals of slope ~-45°, for instance, occur, if we increase N in steps by 12 beginning at N=5.

However, if we look at the points nearest the x-axis (y~0), then we see that there is also another cyclicitiness overlaid: we have a very low point at N=41, then the next lower points follow in steps of 53 up to N=306, where the rhythm breaks such that at N=306+53 we have a very high point instead.

This general behave is simply due to modularity of f(N) mod(log(2)). However, it does not lead to exact periodicity of the distances. The reason for this is the irrationality of the ratio ß=log(3)/log(2) and N.

Anyway, for the analysis of the Collatz-problem, namely for the discussion of the "primitive loop" (or "1-cycle") we are interested in the cases of best approximations. We may say, that cycles are "more likely" for length N, if the distance-measure f(N) is small, or near zero. Well: "likeliness" is not really a correct notion for the cycle-discussion, but it gives here an idea, that we are interested in the sharpest approximations depending on N.

So we define a lower envelope for the f(N)-function by connecting the moving minima of the points when increasing N; in the above plot it is indicated by the blue line.

1.4. The lower envelope for f(N)

We are now interested in the characteristic of that envelope.

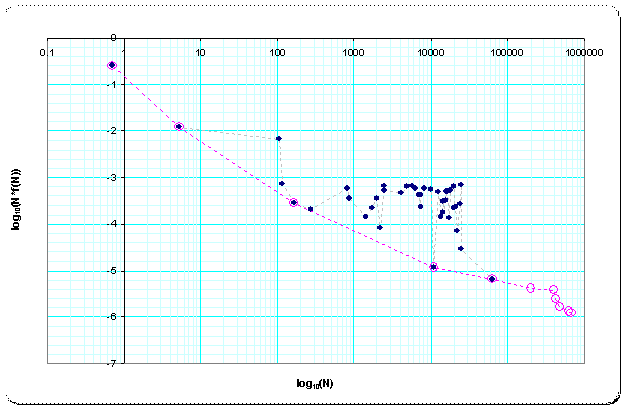
In the following plot I draw that envelope, whose points were determined using the continued-fraction-representation of log(3)/log(2). That representation gives the points N at which minimal values f(N) occur. That method allows to find relevant N up to N=10³⁸ and its values f(N) in a few seconds, so we get enough points for a good overview. Because we deal with huge values of N and also very small values of f(N) I used a logarithmic scale for both values. (For visual comparision I also inserted sample points for some N which are not on the envelope of local minima)

Plot 2:

Surprisingly the general tendency of the lower envelope env_low is linear in this log-scales. This information is new to me; I didn't come across a linear ratio of that logarithms before (in [1] I had some logarithmic/polynomial guess bases on much less N).

The long-scale relation between N and env_low(f(N)) is then, using the above equation for the trend, in some different ways of expression:

                env_low (log₁₀(f(N)))                       ~ –0.994 log₁₀(N) + 0.022
                env_low (log(f(N)))                          ~ – 0.994 log(N) + 0.050657
                env_low ( f(N) )                                   ~ 1.05196 * N^-0.994
                env_low (2^S/3^N )                                                ~ 3 ^{2.606/N^0.994}
                env_low (2^S )                                        ~ 3 ^{N+2.606/N^0.994}

Note: this does not help for the general cycle. The trend in this formulation is also very raw and rather useless for the actual computation of the upperbound for the smallest member of the general cycle. Such computation should be made on the base of the original computation for each N. In table 2.2 I give some example data for cycle-lengthes N=1 to N=100 instead. That table shows the lower bound for a₁ to make a cycle impossible, or said differently: the smallest member of a general cycle must be smaller than the given bound (but all of these small values a₁ are easily checked empirically and none is member of a cycle, so cycles of the indicated lengthes cannot exist. For instance, if a₁=5 is given, no cycle at all is possible – already alone on the discussed approximation argument).

1.5. More values and another hullcurve

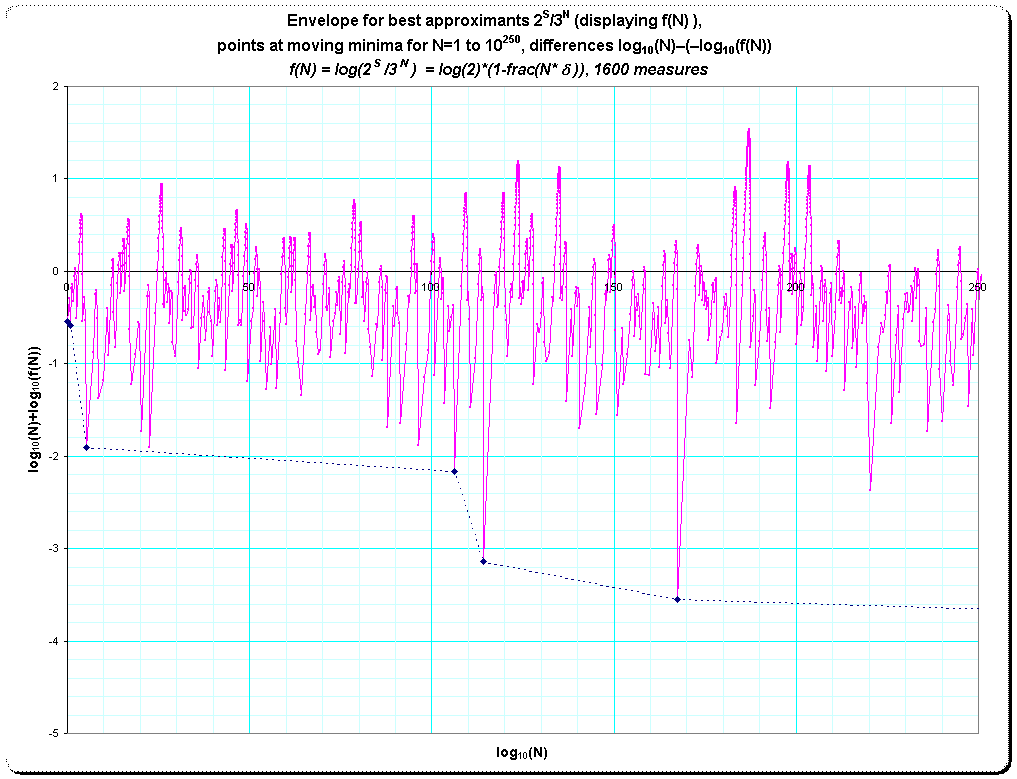
I proceeded using more terms for the hullcurve up to 1600 coordinates which means I arrived at N~10²⁵⁰. Setting precision of computation in Pari/GP to 15000 gives about 14500 entries for the continued fraction of log(3)/log(2). Building the list of convergents gives about 80000 values for N, which gives the coordinates for the hullcurve.

To finally compute with all these values I had then to reduce the precision to 5000 digits (because of memory management) and could effectively check the coordinates up to N~ 10²⁸⁴⁸ distributed in about 25000 entries in that table of convergents. Because log(N) seems in the great overview nearly linear with log(f(N)) I computed the difference of that values log₁₀(N) – (-log₁₀(f(N))) = log₁₀(N*log(2^S/3^N)) . That differences were in a very near range of about –4 to +5 . However, also here we find nonconstant bounds, so there is again the need of a greater overview: to look at a hullcurve connecting that progressive extrema. Here is the Pari/GP-program and then the few coordinates of that hullcurve.

fmt(15000,12)
cfl = cf_convergentslist(log(3)/log(2));
            \\ length(cfl)
            \\ %2414 = 14569               \\ number of coefficients of cont. frac

cf_xopt_chklae( cfl )      \\ check length when list of convergents were expanded to all N with diminuishing intervals
            \\ %2415 = 82099              \\ length of that list, this is too long for current memory allocation!

NList = cf_xopt( cfl , 25000);             \\ create list containing all relevant N
                                           \\ allocated memory allows only to work with about 25000 entries
            \\ VE(NList,5)                        \\ do a short check , show the first few entries N
            \\ %2417 = [1, 3, 5, 17, 29]~ \\ the first few N (for the exponent of 3^N according to the list of convergents

fmt(5000,12)                               \\ precision may be reduced, but must be >2000 (for instance)
[lg10=log(10),lg2=log(2),lg3=log(3),ld3=lg3/lg2] \\ recompute constants with current prec

amin=5;amax=-5;                            \\ loop to find the moving minima of the deviation-function df(N) = log(N) – (-log(f(N))
for(k=1, length( NList) ,
        N = NList [k]; lgN = log(N) ;
        fN = lg2*(1-frac(ld3*N)); lgfN = log(fN) ;

        dfN = lgN – (- lgfN) ;
        if( dfN < amin, amin = dfN;                \\ if dfN has new minimal value, register and print values
              print(k," ",lgN/lg10," ",dfN/lg10)) \\ use log to base 10 for more transparent display
    )

A shorter procedure is needed if the precision (and by this the length of the continued fractions and from this the integer size of the convergents) is increased above, say fmt(20 000) . For precision with 2 million decimal digits of the log₂(3) Pari/GP needed the following procedure.Note that many variables (even temporary ones) are kept as global and outside the function to decrease the memory-requirements in the Pari/GP-stack:

{mkcvgtsN2(maxidx=999)=local(atmp1,atmp2,ui,li,c); \\ maxidx= (#cf>>1)<<1 ;
cfUpHi=cfLoHi=0; ui=li=0;
tmp11=tmp22=1;tmp12=tmp21=0;
forstep(i=1,maxidx,2, \\ if( (i % 10000)==1,print(i));
      c=cf[i];
          atmp1=1*tmp11+c *tmp12;
          atmp2=1*tmp21+c *tmp22;
          if(c>cfUpHi,
              cfUpHi=c;
                ui++;N=NUp[ui]=tmp12+(tmp12==0);IUp[ui]=i;
            );
          tmp11=tmp12; tmp21=tmp22;
          tmp12=atmp1; tmp22=atmp2;

      c=cf[i+1];
          atmp1=1*tmp11+c *tmp12;
          atmp2=1*tmp21+c *tmp22;
          if(c>cfLoHi,
                cfLoHi=c;
                li++;N=NLo[li]=tmp12;if(N==0,N++);ILo[li]=i+1;
            );
          tmp11=tmp12; tmp21=tmp22;
          tmp12=atmp1; tmp22=atmp2;
      );
NUp=vecextract(NUp,Str("1..",ui)); IUp=vecextract(IUp,Str("1..",ui));
NLo=vecextract(NLo,Str("1..",li)); ILo=vecextract(ILo,Str("1..",li));
print("ok - NUp,NLo "); }
\\ =========================== end procedures =====================================================

and then the environment for and the call of that function:

allocatemem(240 000 000)
fmt(2 000 000 );ld3=log(3)/log(2)

cf=contfrac(ld3);
fmt(200); #cf

l2=log(2);l10=log(10);

NUp=NLo=IUp=ILo=vector(2000);
mkcvgtsN2( (#cf >>1) <<1)

{ print("for S > N ");
       for(ui=2,#NUp, N=NUp[ui];
             print([ui,IUp[ui], lN=log(N)/l10,
                   lK=log(l2 * (1-frac(ld3*N)))/l10 ,
                   lK1=lN+lK,
                   lK1+if(lN>0,log(lN)/l10 )
                   ])
          )

print("for S < N ");
       for(li=1,#NLo, N=NLo[li];
             print([li,ILo[li],lN=log(N)/l10,
                    lK=log(l2 * ( frac(ld3*N)))/l10 ,
                    lK1=lN+lK,
                    lK1+if(lN>0,log(lN)/l10 )
                   ])
           )
    }

Table 1.3: Coordinates for hullcurve characterizing N*f(N) using D_N=log₁₀(N * log(2^S/3^N))=log₁₀(N)+log₁₀(log(2)*(1-{ßN}))

index k	index into cf convgts	log₁₀(N)	D_N=log₁₀(N)–(–log₁₀(f(N))) =log₁₀(N∙f(N))	nn= log₁₀(log₁₀(N))	dd= nn+D_N	coeff in cont frac at index+1	index into version 1 list of N
1	2	0.0	-0.541087201293			1	1
2	4	0.698970004336	-0.584058910762	-0.1555	-0.7396	2	3
3	14	5.27997932298	-1.91041044730	0.7226	-1.1878	55	37
4	218	106.118391607	-2.16096110843	2.0258	-0.1352	100	542
5	230	114.250602011	-3.14344653731	2.0579	-1.0856	964	597
6	330	167.420643539	-3.54599907505	2.2238	-1.3222	2 436	971
7	528	272.363973245	-3.67896692796	2.4351	-1.2438	3 308	1730
8	2764	1407.08628196	-3.84754329367	3.1483	-0.6992	4 878	9591
9	4312	2234.17531188	-4.07448957185	3.3491	-0.7254	8 228	19795
10	21 150	10853.91593	-4.934419822	4.0356	-0.8988	59 599	^-------(*1)
11	^(*2)122 416	63113.10582	-5.179259315	4.8001	-0.3791	104 733
12	^(*3) 396 190	204217.496	-5.37392218	5.3101	-0.0638	163 963
13	771 792	397616.664	-5.4202135	5.5995	0.1793	182 405
14	819 418	422115.224	-5.6030959	5.6254	0.0223	277 920
15	918 630	473290.39	-5.7783013	5.6751	-0.1032	416 031
15	1 228 670	632954.726	-5.87482624	5.8014	-0.0735	519 578
17	1 328 536	684406.16	-5.92158166	5.8353	-0.0863	578 637

Note: ^(*1) (21.Mar 12) I computed the new values by a shorter routine and another list, so the list-index was not comparable

Note: ^(*2) (21.Sep 12): the length of the cont-frac-coefficients was 193 862 given float precision 200 000 dec digits in Pari/Gp

Note: ^(*3) (21.Nov 17): the length of the cont-frac-coefficients was 1 940 942 given float precision 2 000 000 dec digits in Pari/Gp

The graphic with the currently farthest view contains several low values of the criterion (blue dots) and the currently best hullcurve for the lowest values (magenta dots/line) taken as piecewise linear graph:

According to this, up to N~10^63113.11 (that N has more than 63000 digits) we have

                log₁₀(N∙log(2^S/3^N) > -5.2
                N∙log(2^S/3^N) > 10^-5.2
                log(2^S/3^N) > 10^{-5.2-log10(N)} ~ 0.00000662216503702/N
                S log(2)-N log(3) > 10^{-5.2-log10(N)}

                log(2^S/3^N) > 1/(N*10^5.07 )

where it is not yet recognizable which form (linear, parabolic, logarithmic,…) that hullcurve shows in a even longer scale. (If we use the log₁₀ of log₁₀(N) again, it looks as if we have again a bound roughly linear with that values…)

A more recent heuristic using N up to 10^685
000 (that N has more than 685 000 digits) gives

Guessed optimized functional lower bound

log₁₀(N∙log(2^S/3^N) + log₁₀(log₁₀(N))^0.8   > -2                observed

                log₁₀(N∙log(2^S/3^N)   > -2 - log₁₀(log₁₀(N))^0.8
                log(2^S/3^N) > 1/100/N/10^(log₁₀(log₁₀(N))^0.8 )

                S log(2)-N log(3) > 1/100/N/10^(log₁₀(log₁₀(N))^0.8 )

                               N=10                    1/N/100
                               N=100                1/N/241
                               N=200                1/N/277
                               N=1000               1/N/357
                               N=10000            1/N/464
                               log₁₀(N)=6         1/N/563
                               log₁₀(N)=10      1/N/1000
                               log₁₀(N)=20      1/N/1700
                               log₁₀(N)=100   1/N/5510                ~2/100/N/log₁₀(N)
                               log₁₀(N)=10³    1/N/25510                ~4/100/N/log₁₀(N)
                               log₁₀(N)=10⁴    1/N/107500                ~9/100/N/log₁₀(N)
                               log₁₀(N)=10⁵                                    ~25/100/N/log₁₀(N)
                               log₁₀(N)=10⁶                                    ~64/100/N/log₁₀(N)
                               log₁₀(N)=10⁷                                    ~180/100/N/log₁₀(N)

We can put now that (newest) heuristic and the condition for a cycle together. Remember, the cycle with N elements a₁,a₂,...a_k,...a_N must satisfy the condition

2^S = (3 + 1/a₁)(3 + 1/a₂)...(3 + 1/a_k)...(3 + 1/a_N)

If we assume that a₁ is the smallest element then an upper bound for a₁ , dependend on N, can then be determined.

We reduce all a_k to the value of a₁ then the rhs is surely larger than the original expression. We can then write

                2^S < (3 + 1/a₁)^N
                S log(2) < N log (3 + 1/a₁) = N log (3) + N log(1 + 1/3/a₁)
                S log(2) − N log (3) < N log(1 + 1/3/a₁)

For the lhs we have just found a heuristical lower bound such that we can write the concatenated inequality

1/100/N/10^(log₁₀(log₁₀(N))^0.8 ) < log(2)∙(1-frac(ß∙N)) =S log(2) − N log(3) < N∙log(1+1/(3a₁))
1/100/N/10^(log₁₀(log₁₀(N))^0.8 ) < N∙log(1+1/(3a₁))

Now we use, that log(1+1/x) is near, but always smaller than 1/x so we look at:

1/100/N/10^(log₁₀(log₁₀(N))^0.8 ) < N∙1/(3a₁)
a₁ < 33.3 N² ∙ 10^(log₁₀(log₁₀(N))^0.8 )

and get an upper bound for a₁ depending on the length N of a projected cycle. A short table for examples:

N	a1
10	< 3 333.333...
100	< 804 645.550972
1000	< 119 153 085.026

Of course, for small N like these we can evaluate the upper bound for the smallest member a₁ by direct formulae - we simply use

2^S < ( 3+1/a₁) ^N
a₁< 1/( 2^S/N-3 )

Conversely, if we use the knowledge, that all a₁<5∙2⁶⁰ are not member of a nontrivial cycle, then we can compute a lower bound for the length N of a cycle; we get by numerical search

N > 142 793 282 if a₁>5∙2⁶⁰

To compare: the best proven lower bound for f(N)= log(2)*S - log(3)*N > 0 seems to be

| f(N) | > e^{-13.3(0.46057+log(N))} ~ 1/457/N^13.3

which is due to G.Rhin (1987) as cited in J. Simons (2007) . Of course, this bound is rather weak; we find, that for a₁=5∙2⁶⁰ the length of a cycle must be greater than 14.43 .

The general form is also be described and a bit explained in T. Tao's blog, which results in

| f(N) | > t /S ^u where S = ceil (N* log(3)/log(2))

Empirically, that exponent u is very near 1 and thus the formula above, having N^13.3 in the denominator, is very weak. It can -however- be used for the disproof of the 1-cycle, because the 1-cycle puts hard restrictions on its members which can be nicely exploited for a disproof.

Gottfried Helms, 11'2017 (previous version: 9'2012, 3'2012, 3'2010)

for a overview of the related cycle-discussion ("primitive loop") see:

[1] "cycles in the collatz-iteration",
G. Helms, 2006-2008
http://go.helms-net.de/math/collatz/Collatz061102.pdf

[2] "disproving the 1-cycle",
G. Helms, 11'2017
http://go.helms-net.de/math/collatz/Collatz_1cycledisproof.pdf

[Simons,2005]Theoretical and computational bounds for m-cycles of the 3n + 1 problem
J. Simons; Benne de Weger,
Acta Arithmetica, Vol. 117, pp. 51–70, 2005.
Online update 2010 http://deweger.xs4all.nl/papers/%5b35a%5dSidW-3n+1-v1.44%5b2010%5d.pdf
Future updates may appear on http://www.win.tue.nl/∼bdeweger/research.html .

[3] number ß=log(3)/log(2) to 1 million digits, in Pari/GP-textformat
http://go.helms-net.de/math/collatz/ld3.zip
continued fraction of ß to 145 000 coefficients
http://go.helms-net.de/math/collatz/cf32.zip

2. Appendix

How to read the following table:

N	f(N)=log(2^S/3^N)	log₁₀(N)	log₁₀(f(N))	3^N	3^N*exp(f(N))=2^S
length of the cycle (T()-transformations)= 1	0.287682072452	0.000000	-0.541087201293	3^1 = 3	3*exp(f(N))=4
length of the cycle (T()-transformations)= 3	0.169899036795	0.477121254720	-0.769809083259	3^3 = 27	27*exp(f(N))=32
length of the cycle (T()-transformations)= 5	0.0521160011390	0.698970004336	-1.28302891510	3^5 =243	243*exp(f(N))=256
17	0.0385649677607	1.23044892138	-1.41380702736	…	…

2.1. Data for graph of envelope:

N	f(N)	log₁₀(N)	log₁₀(f(N))	log₁₀(N)+log₁₀(f(N))
1	0.287682072452	0.000000	-0.541087201293	-0.54108720129
3	0.169899036795	0.477121254720	-0.769809083259	-0.29268782854
5	0.0521160011390	0.698970004336	-1.28302891510	-0.58405891076
17	0.0385649677607	1.23044892138	-1.41380702736	-0.18335810598
29	0.0250139343823	1.46239799790	-1.60181799375	-0.13941999585
41	0.0114629010039	1.61278385672	-1.94070545824	-0.32792160152
94	0.00937476862954	1.97312785360	-2.02803944191	-0.05491158831
147	0.00728663625513	2.16731733475	-2.13747290968	0.02984442507
200	0.00519850388072	2.30102999566	-2.28412162749	0.01690836817
253	0.00311037150632	2.40312052118	-2.50718773525	-0.10406721407
306	0.00102223913191	2.48572142648	-2.99044749802	-0.50472607154
971	0.000978585021321	2.98721922991	-3.00940143604	-0.02218220613
1636	0.000934930910732	3.21378329934	-3.02922048132	0.18456281802
2301	0.000891276800144	3.36191661867	-3.04998739798	0.31192922069
2966	0.000847622689555	3.47217114669	-3.07179742641	0.40037372028
3631	0.000803968578966	3.56002624891	-3.09476092420	0.46526532471
4296	0.000760314468378	3.63306427269	-3.11900674504	0.51405752765
4961	0.000716660357789	3.69556922704	-3.14468661795	0.55088260909
5626	0.000673006247200	3.75019972783	-3.17198090441	0.57821882342
6291	0.000629352136612	3.79871968519	-3.20110628906	0.59761339613
6956	0.000585698026023	3.84235957333	-3.23232623967	0.61003333366
7621	0.000542043915434	3.88201196163	-3.26596552627	0.61604643536
8286	0.000498389804846	3.91834492896	-3.30243085027	0.61591407869
8951	0.000454735694257	3.95187155713	-3.34224095472	0.60963060241
9616	0.000411081583668	3.98299445466	-3.38607197905	0.59692247561
10281	0.000367427473080	4.01203535915	-3.43482837399	0.57720698516
10946	0.000323773362491	4.03925544381	-3.48975888442	0.54949655939
11611	0.000280119251902	4.06486962506	-3.55265704217	0.51221258289
12276	0.000236465141314	4.08905687976	-3.62623287205	0.46282400771
12941	0.000192811030725	4.11196783721	-3.71486812372	0.39709971349
13606	0.000149156920136	4.13373046662	-3.82635659274	0.30737387388
14271	0.000105502809548	4.15445440614	-3.97673597492	0.17771843122
14936	0.0000618486989592	4.17423430494	-4.20866943170	-0.03443512676
15601	0.0000181945883705	4.19315243685	-4.74005776533	-0.54690532848
47468	0.0000109296545229	4.67640093369	-4.96139356551	-0.28499263182
79335	0.00000366472067521	4.89946482607	-5.43595912166	-0.53649429559
190537	0.0000000645075027718	5.27997932298	-7.19038977028	-1.91041044730
10781274	0.0000000122069827808	7.03267008353	-7.91339166804	-0.88072158451
64497107	0.00000000873439391323	7.80954023491	-8.05876722569	-0.24922699078
118212940	0.00000000526180504562	8.07266501853	-8.27886524693	-0.20620022840
171928773	0.00000000178921617802	8.23534856377	-8.74733718361	-0.51198861984
397573379	1.05843488432E-10	8.59941729690	-9.97533585493	-1.37591855803
6586818670	1.01231253207E-11	9.81867570782	-10.9946853867	-1.17600967888
72057431991	5.51089009577E-12	10.8576787805	-11.2587782501	-0.40109946960
137528045312	8.98654870862E-13	11.1383912704	-12.0464070674	-0.90801579700
890638885193	7.79694000263E-13	11.9497016525	-12.1080758077	-0.15837415520
1643749725074	6.60733129664E-13	12.2158356932	-12.1799739168	0.03586177640
2396860564955	5.41772259065E-13	12.3796427701	-12.2661832364	0.11345953370
3149971404836	4.22811388467E-13	12.4983066113	-12.3738533234	0.12445328790
3903082244717	3.03850517868E-13	12.5914077027	-12.5173400191	0.07406768360
4656193084598	1.84889647269E-13	12.6680309815	-12.7330874061	-0.06505642460
5409303924479	6.59287766701E-14	12.7331413832	-13.1809249827	-0.44778359950
11571718688839	1.28966827413E-14	13.0633978673	-13.8895219837	-0.82612411640
64021008208555	1.14513197778E-14	13.8063225092	-13.9411444575	-0.13482194830
116470297728271	1.00059568144E-14	14.0662151856	-13.9997413759	0.06647380970
168919587247987	8.56059385088E-15	14.2276800116	-14.0674961071	0.16018390450
221368876767703	7.11523088740E-15	14.3451165614	-14.1478110026	0.19730555880
273818166287419	5.66986792391E-15	14.4374622577	-14.2464270576	0.19103520010
326267455807135	4.22450496043E-15	14.5135737564	-14.3742241756	0.13934958080
378716745326851	2.77914199695E-15	14.5783145083	-14.5560892629	0.02222524540
431166034846567	1.33377903347E-15	14.6346445419	-14.8749161138	-0.24027157190
914781359212850	1.22219510347E-15	14.9613173063	-14.9128594605	0.04845784580
1398396683579133	1.11061117346E-15	15.1456303853	-14.9544379616	0.19119242370
1882012007945416	9.99027243451E-16	15.2746223901	-15.0004226684	0.27419972170
2365627332311699	8.87443313444E-16	15.3739463294	-15.0518593785	0.32208695090
2849242656677982	7.75859383436E-16	15.4547294376	-15.1102169830	0.34451245460
3332857981044265	6.64275453429E-16	15.5228168080	-15.1776517955	0.34516501250
3816473305410548	5.52691523421E-16	15.5816622290	-15.2575171961	0.32414503290
4300088629776831	4.41107593414E-16	15.6334774070	-15.3554554660	0.27802194100
4783703954143114	3.29523663407E-16	15.6797642949	-15.4821133929	0.19765090200
5267319278509397	2.17939733399E-16	15.7215896439	-15.6616635847	0.05992605920
5750934602875680	1.06355803392E-16	15.7597384290	-15.9732388075	-0.21350037850
11985484530117643	1.01127676776E-16	16.0786555957	-15.9951299698	0.08352562590
18220034457359606	9.58995501609E-17	16.2605491940	-16.0181834300	0.24236576400
24454584384601569	9.06714235454E-17	16.3883602862	-16.0425295658	0.34583072040
30689134311843532	8.54432969300E-17	16.4869846379	-16.0683220022	0.41866263570
36923684239085495	8.02151703145E-17	16.5673050283	-16.0957434901	0.47156153820
43158234166327458	7.49870436990E-17	16.6350636671	-16.1250137678	0.51004989930
49392784093569421	6.97589170835E-17	16.6936635065	-16.1564002699	0.53726323660
55627334020811384	6.45307904680E-17	16.7452882466	-16.1902330150	0.55505523160
61861883948053347	5.93026638525E-17	16.7914231419	-16.2269257979	0.56449734400
68096433875295310	5.40745372370E-17	16.8331243691	-16.2670071885	0.56611718060
74330983802537273	4.88464106215E-17	16.8711698809	-16.3111673440	0.56000253690
80565533729779236	4.36182840061E-17	16.9061492886	-16.3603314241	0.54581786450
86800083657021199	3.83901573906E-17	16.9385201437	-16.4157801074	0.52274003630
93034633584263162	3.31620307751E-17	16.9686446515	-16.4793588820	0.48928576950
99269183511505125	2.79339041596E-17	16.9968144498	-16.5538683612	0.44294608860
105503733438747088	2.27057775441E-17	17.0232678282	-16.6438636214	0.37940420680
111738283365989051	1.74776509286E-17	17.0482019950	-16.7575169388	0.29068505620
117972833293231014	1.22495243131E-17	17.0717820098	-16.9118807760	0.15990123380
124207383220472977	7.02139769766E-18	17.0941474122	-17.1535764275	-0.05942901530
130441933147714940	1.79327108217E-18	17.1154172264	-17.7463540548	-0.63093682840
397560349370386783	1.51686631025E-19	17.5994030636	-18.8190526943	-1.21964963070
4640282259296926456	2.69684901278E-20	18.6665443986	-19.5691433675	-0.90259896890
27444133206411171953	1.01243097420E-20	19.4384495186	-19.9946345766	-0.55618505800
77692117359936589403	3.40443909807E-21	19.8903769575	-20.4679544305	-0.57757747300
205632218873398596256	8.90075522457E-23	20.3130911618	-22.0505731421	-1.73748198030
7941964418702608664581	6.68554395133E-23	21.8999279370	-22.1748632518	-0.27493531480
15678296618531818732906	4.47033267809E-23	22.1952988766	-22.3496601559	-0.15436127930
23414628818361028801231	2.25512140485E-23	22.3694872775	-22.6468300728	-0.27734279530
31150961018190238869556	3.99101316135E-25	22.4934714493	-24.3989168400	-1.90544539070
1752190149218482586763461	1.97560971162E-25	24.2435812344	-24.7042988476	-0.46071761320
5225419486637257521420827	1.93581597351E-25	24.7181211605	-24.7131359309	0.00498522960
8698648824056032456078193	1.89602223540E-25	24.9394517982	-24.7221565738	0.21729522440
12171878161474807390735559	1.85622849729E-25	25.0853575965	-24.7313685642	0.35398903230
15645107498893582325392925	1.81643475919E-25	25.1943785516	-24.7407801961	0.45359835550
19118336836312357260050291	1.77664102108E-25	25.2814501090	-24.7504003146	0.53104979440
22591566173731132194707657	1.73684728297E-25	25.3539463397	-24.7602383664	0.59370797330
26064795511149907129365023	1.69705354486E-25	25.4160543221	-24.7703044548	0.64574986730
29538024848568682064022389	1.65725980675E-25	25.4703814515	-24.7806094024	0.68977204910
33011254185987456998679755	1.61746606865E-25	25.5186620247	-24.7911648212	0.72749720350
36484483523406231933337121	1.57767233054E-25	25.5621082027	-24.8019831911	0.76012501160
39957712860825006867994487	1.53787859243E-25	25.6016006217	-24.8130779485	0.78852267320
43430942198243781802651853	1.49808485432E-25	25.6377992511	-24.8244635867	0.81333566440
46904171535662556737309219	1.45829111621E-25	25.6712114695	-24.8361557699	0.83505569960
50377400873081331671966585	1.41849737810E-25	25.7022357571	-24.8481714626	0.85406429450
53850630210500106606623951	1.37870364000E-25	25.7311907902	-24.8605290778	0.87066171240
57323859547918881541281317	1.33890990189E-25	25.7583354232	-24.8732486466	0.88508677660
60797088885337656475938683	1.29911616378E-25	25.7838827847	-24.8863520136	0.89753077110
64270318222756431410596049	1.25932242567E-25	25.8080104502	-24.8998630628	0.90814738740
67743547560175206345253415	1.21952868756E-25	25.8308679358	-24.9138079791	0.91705995670
71216776897593981279910781	1.17973494945E-25	25.8525823146	-24.9282155545	0.92436676010
74690006235012756214568147	1.13994121135E-25	25.8732624957	-24.9431175454	0.93014495030
78163235572431531149225513	1.10014747324E-25	25.8930025287	-24.9585490944	0.93445343430
81636464909850306083882879	1.06035373513E-25	25.9118841903	-24.9745492295	0.93733496080
85109694247269081018540245	1.02055999702E-25	25.9299790303	-24.9911614587	0.93881757160
88582923584687855953197611	9.80766258914E-26	25.9473500096	-25.0084344835	0.93891552610
92056152922106630887854977	9.40972520806E-26	25.9640528215	-25.0264230591	0.93762976240
95529382259525405822512343	9.01178782697E-26	25.9801369694	-25.0451890418	0.93494792760
99002611596944180757169709	8.61385044589E-26	25.9956466510	-25.0648026728	0.93084397820
102475840934362955691827075	8.21591306481E-26	26.0106214909	-25.0853441648	0.92527732610
105949070271781730626484441	7.81797568373E-26	26.0250971500	-25.1069056847	0.91819146530
109422299609200505561141807	7.42003830264E-26	26.0391058376	-25.1295938529	0.90951198470
112895528946619280495799173	7.02210092156E-26	26.0526767427	-25.1535329331	0.89914380960
116368758284038055430456539	6.62416354048E-26	26.0658364002	-25.1788689540	0.88696744620
119841987621456830365113905	6.22622615940E-26	26.0786090033	-25.2057751082	0.87283389510
123315216958875605299771271	5.82828877832E-26	26.0910166714	-25.2344589381	0.85655773330
126788446296294380234428637	5.43035139723E-26	26.1030796799	-25.2651720664	0.83790761350
130261675633713155169086003	5.03241401615E-26	26.1148166605	-25.2982236367	0.81659302380
133734904971131930103743369	4.63447663507E-26	26.1262447734	-25.3339993030	0.79224547040
137208134308550705038400735	4.23653925399E-26	26.1373798590	-25.3729887652	0.76439109380
140681363645969479973058101	3.83860187290E-26	26.1482365693	-25.4158269291	0.73240964020
144154592983388254907715467	3.44066449182E-26	26.1588284842	-25.4633576745	0.69547080970
147627822320807029842372833	3.04272711074E-26	26.1691682135	-25.5167369959	0.65243121760
151101051658225804777030199	2.64478972966E-26	26.1792674870	-25.5776088502	0.60165863680
154574280995644579711687565	2.24685234858E-26	26.1891372350	-25.6484254662	0.54071176880
158047510333063354646344931	1.84891496749E-26	26.1987876589	-25.7330830618	0.46570459710
161520739670482129581002297	1.45097758641E-26	26.2082282948	-25.8383392962	0.36988899860
164993969007900904515659663	1.05304020533E-26	26.2174680698	-25.9775550470	0.23991302280
168467198345319679450317029	6.55102824247E-27	26.2265153535	-26.1836905283	0.04282482520
171940427682738454384974395	2.57165443165E-27	26.2353780027	-26.5897873905	-0.35440938780
347354084702895683704606156	1.16393505247E-27	26.5407724103	-26.9340712526	-0.39329884230
870121826425948596728844073	9.20150725772E-28	26.9395800628	-27.0361410270	-0.09656096420
1392889568149001509753081990	6.76366399071E-28	27.1439166858	-27.1698179757	-0.02590128990
1915657309872054422777319907	4.32582072370E-28	27.2823178212	-27.3639314831	-0.08161366190
2438425051595107335801557824	1.88797745669E-28	27.3871094115	-27.7240031957	-0.33689378420
5399617844913267584627353565	1.33811164637E-28	27.7323630239	-27.8735076494	-0.14114462550
8360810638231427833453149306	7.88245836047E-29	27.9222483873	-28.1033383148	-0.18108992750
11322003431549588082278945047	2.38380025725E-29	28.0539232822	-28.6227301377	-0.56880685550
36927203087966924495662630882	1.65274266854E-29	28.5673464149	-28.7817947607	-0.21444834580
62532402744384260909046316717	9.21685079830E-30	28.7961051163	-29.0354174428	-0.23931232650
88137602400801597322430002552	1.90627491119E-30	28.9451612323	-29.7198144679	-0.77465323560
378155609259623725703103696043	3.14523757646E-31	29.5776705468	-30.5023465444	-0.92467599760
2558951662416564482599295869749	2.95391392334E-31	30.4080620823	-30.5296021641	-0.12154008180
4739747715573505239495488043455	2.76259027021E-31	30.6757552259	-30.5586835221	0.11707170380
6920543768730445996391680217161	2.57126661709E-31	30.8401402197	-30.5898528886	0.25028733110
9101339821887386753287872390867	2.37994296396E-31	30.9591053302	-30.6234334508	0.33567187940
11282135875044327510184064564573	2.18861931084E-31	31.0523913258	-30.6598297732	0.39256155260
13462931928201268267080256738279	1.99729565771E-31	31.1291396499	-30.6995576422	0.42958200770
15643727981358209023976448911985	1.80597200459E-31	31.1943402557	-30.7432889862	0.45105126950
17824524034515149780872641085691	1.61464835146E-31	31.2510179418	-30.7919220465	0.45909589530
20005320087672090537768833259397	1.42332469834E-31	31.3011455045	-30.8466960145	0.45444949000
22186116140829031294665025433103	1.23200104521E-31	31.3460812821	-30.9093889237	0.43669235840
24366912193985972051561217606809	1.04067739209E-31	31.3868004983	-30.9826838800	0.40411661830
26547708247142912808457409780515	8.49353738964E-32	31.4240270362	-31.0709113971	0.35311563910
28728504300299853565353601954221	6.58030085840E-32	31.4583130158	-31.1817542495	0.27655876630
30909300353456794322249794127927	4.66706432715E-32	31.4900891747	-31.3309562131	0.15913296160
33090096406613735079145986301633	2.75382779590E-32	31.5196980325	-31.5600632208	-0.04036518830
35270892459770675836042178475339	8.40591264657E-33	31.5474164488	-32.0754151275	-0.52799867870
107993473432468968265022727599723	6.08537262725E-33	32.0333975098	-32.2157128233	-0.18231531350
180716054405167260694003276724107	3.76483260793E-33	32.2569967360	-32.4242543286	-0.16725759260
253438635377865553122983825848491	1.44429258861E-33	32.4038728215	-32.8403448173	-0.43647199580
579599851728429398674948200821366	5.68045157903E-34	32.7631282657	-33.2456171378	-0.48248887210
1485360919807422642901860776615607	2.59842885097E-34	33.1718319933	-33.5852891703	-0.41345717700
3876482907693838530030634129025455	2.11483497389E-34	33.5884378734	-33.6747235161	-0.08628564270
6267604895580254417159407481435303	1.63124109681E-34	33.7971016111	-33.7874818457	0.00961976540
8658726883466670304288180833845151	1.14764721972E-34	33.9374540412	-33.9401915911	-0.00273754990
11049848871353086191416954186254999	6.64053342637E-35	34.0433563382	-34.1777970329	-0.13444069470
13440970859239502078545727538664847	1.80459465553E-35	34.1284306395	-34.7436203332	-0.61518969370
42714034565604922122765955968404389	5.77845195764E-36	34.6305705948	-35.2381884931	-0.60761789830
157415167403180186412518096334952709	5.06786127522E-36	35.1970465756	-35.2951752818	-0.09812870620
272116300240755450702270236701501029	4.35727059279E-36	35.4347545576	-35.3607854689	0.07396908870
386817433078330714992022377068049349	3.64667991037E-36	35.5875060386	-35.4381023555	0.14940368310
501518565915905979281774517434597669	2.93608922794E-36	35.7002870150	-35.5322307503	0.16805626470
616219698753481243571526657801145989	2.22549854552E-36	35.7897355773	-35.6525726852	0.13716289210
730920831591056507861278798167694309	1.51490786309E-36	35.8638703397	-35.8196137802	0.04425655950
845621964428631772151030938534242629	8.04317180668E-37	35.9271762549	-36.0945726544	-0.16739639950
960323097266207036440783078900790949	9.37264982439E-38	35.9824173744	-37.0281376085	-1.04572023410
7797285910967231555816016771572875912	3.92213035268E-38	36.8919434592	-37.4064779766	-0.51453451740
22431534635635487631007267235817836787	2.39374123364E-38	37.3508589865	-37.6209227992	-0.27006381270

2.2. Table 2: upper bound for the minimal member "a" of an assumed general cycle of length N (also based on the assumtion of maximal density of set of members)

"Maximal density of members" means, the elements (a₁,a₂,… a_n)=(5,7,11,13,…,a_n) or (a₁,a₂,… a_n)=(7,11,13,…,a_n) or similarly, generally of the form a_k+2 = a_k+6 and a_k+1=a_k+2 or a_k+1 = a_k+4. To make a cycle possible at all, its minimal member a₁ must be smaller than the upper bound a₁ given in the table. The higher the upper bound, the "easier" it is for a cycle to exist:

N (cycle length)	upper bound a₁	N (cycle length)	upper bound a₁
1	5	51	83
2	5	52	5
3	5	53	5
4	5	54	17
5	25	55	5
6	5	56	47
7	5	57	5
8	5	58	307
9	5	59	11
10	23	60	5
11	5	61	31
12	5	62	5
13	5	63	125
14	5	64	5
15	17	65	5
16	5	66	23
17	121	67	5
18	5	68	67
19	5	69	5
20	11	70	541
21	5	71	17
22	53	72	5
23	5	73	41
24	5	74	5
25	11	75	185
26	5	76	11
27	31	77	5
28	5	78	25
29	347	79	5
30	5	80	95
31	5	81	5
32	23	82	1073
33	5	83	17
34	103	84	5
35	5	85	55
36	5	86	5
37	17	87	271
38	5	88	11
39	53	89	5
40	5	90	37
41	1133	91	5
42	11	92	131
43	5	93	11
44	31	94	3203
45	5	95	23
46	181	96	5
47	11	97	73
48	5	98	5
49	23	99	401
50	5	100	17

2.3. Envelope for more coordinates (1600 coordinates up to N=10²⁵⁰)

2.4. Envelopes for other problem-configuration: 2^S/3^N, 2^S/5^N , 2^S/11^N

It was interesting,how the envelopes of other configurations would behave. Surprise: they all have the same slope in the trend. That means, the rate-of-approximation is much related.

Plot 3: Envelope-curve for approximation 2^S/3^N, 2^S/5^N, 2^S/11^N

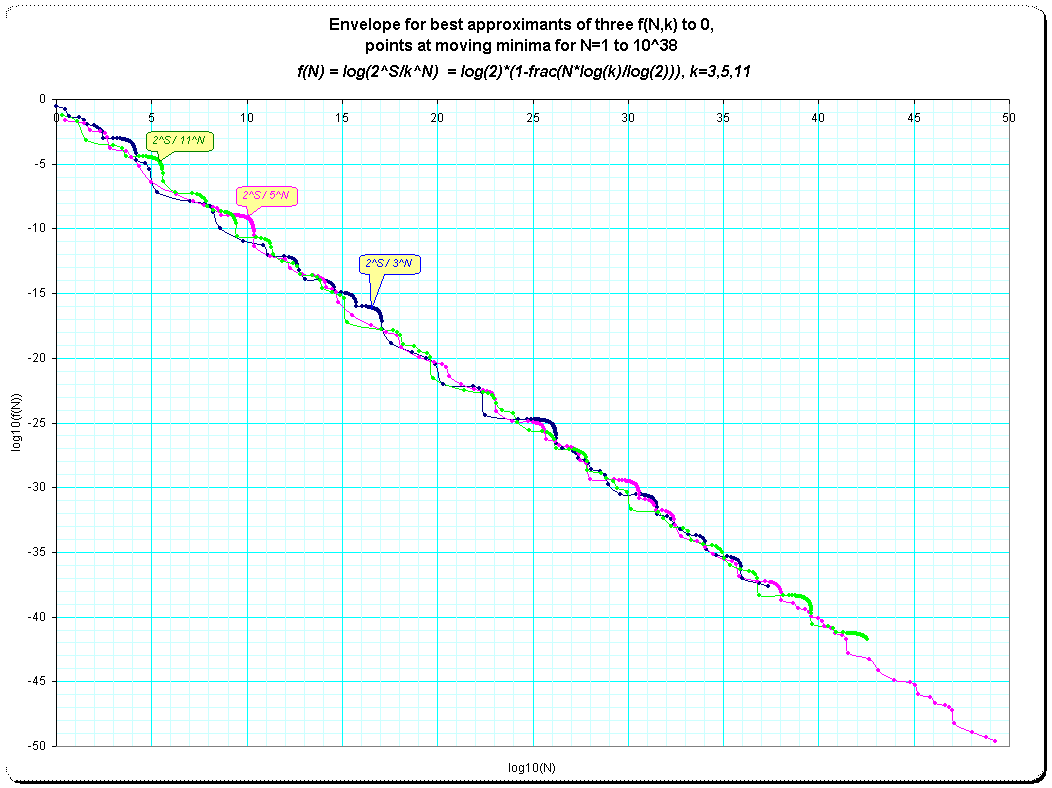
The longer line for k=5 indicates, that this configuration approximates faster to zero

To see the deviation from the trend (with slope –1) I rotate the whole plot by –45° :

Plot 4:Envelope-curves, rotated by 45°

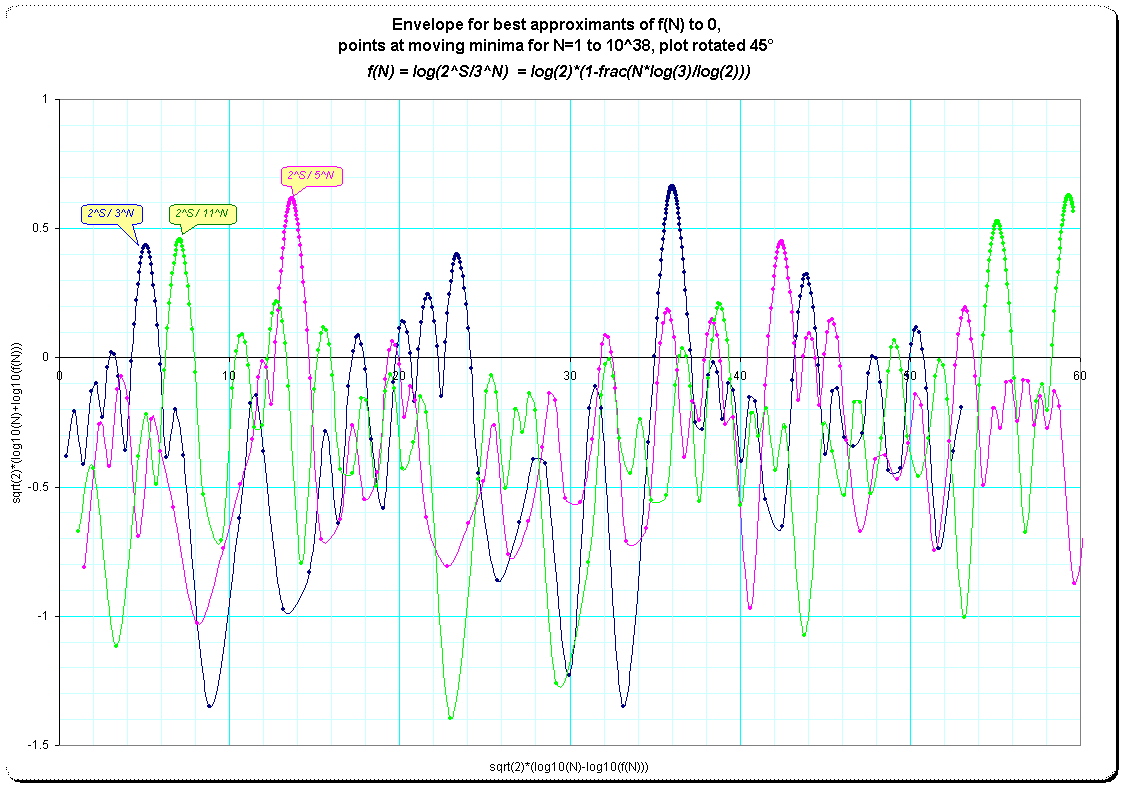
The plot gives the impression as if the curves could be separated using fourier-analysis; but I don't have experience with this.

2.5. An earlier discussion in sci.math research (may 2004)

I took only the relevant posts, also shortened (or even removed) needless quoting of previous post and formatted text to special style. Use the google-link to look at the original posts.

http://groups.google.de/group/sci.math.research/browse_frm/thread/3fe481e4d991d6da/bdc7f0126c4c3e1a

newsgroups: sci.math.research

Betreff: 3^n - 2^n and relatives

Von: Gottfried Helms he...@uni-kassel.de
Datum: Fri, 21 May 2004 13:30:01 +0000 (UTC)

Hi -

I got an unequality, which i'm unable to analytically to disprove. Does anyone know useful related material?

The inequality, formulating a restriction, arose whily studying the question of a certain, primitive assumed loop in the collatz (3x+1)-problem. Here it goes:

3^L - 1

powceil2( 3^L ) <= 2^L* -------

2^L - 1

where powceil2 ( x) = smallest power 2^S >= x

Empirically the lhs is always *greater* than the rhs (up to L=200) The benefit of this inequality is, that if it cannot be satisfied, then a primitive loop in the Collatz-problem cannot exist.

One can reformulate this formula for instance to:

3^L 3^L - 1

powceil2( ---- ) <= ----------

2^L 2^L - 1

or many other ways... I didn't find a definitve form, where I could directly conclude the impossibility of that inequality.

Someone with an idea?

Regards -
Gottfried Helms

Von: Gareth McCaughan gareth.mccaug...@pobox.com
Datum: Sun, 23 May 2004 23:00:01 +0000 (UTC)

Gottfried Helms <he...@uni-kassel.de> writes:

> I got an unequality, which i'm unable to analytically to disprove.

> Does anyone know useful related material?

> The inequality, formulating a restriction, arose whily studying

> the question of a certain, primitive assumed loop in the collatz

> (3x+1)-problem. Here it goes:

> 3^L - 1

> powceil2( 3^L ) <= 2^L* -------

> 2^L - 1

> where powceil2 ( x) = smallest power 2^S >= x

According to theorems mentioned at the start of chapter 3 of Baker's "Transcendental Number Theory", the following is true.

Let A1, ..., An >= 4 and B >= 2, and suppose that ...
a1,...,an are algebraic numbers with height(ak) <= Ak
b1,...,bn are rational integers with |bk| <= B.

Write

F := b1 log a1 + ... + bn log an.

Then either

F=0 or |F| > B^-(C Q log Q),

where

Q = product(log Ak) and
C depends only on n and on d, the maximum degree of the ak.

In particular,

                let n=2 and d=1;
                let a1=2, a2=3; and write
                p = b1, q = -b2.

Then this says

F = |p log 2 - q log 3|
either F = 0 or |F| > max(p,q)^-C

for a constant C.

C can be found explicitly. Baker's book doesn't give details of how, but they are out there in the literature. There have been advances in this area since Baker's book. (Search Google for "laurent mignotte nesterenko".) The value of C will still be much larger than you'd like :-).

Anyway: if the inequality above (the one you want to prove can't happen) holds then you can find p,q with |F| <= 2^-p or something like that. And if F is small then p and q have to be somewhat similar in size.

Now, if p^-C < F <= 2^-p then -C log p <= -p log 2, so p / log p <= C / log 2. So you can get an upper bound on the size of p. It may or may not be practical then to check all actual values of p up to there.

A nasty back-of-envelope calculation using a version of Laurent-Mignotte-Nestorenko quoted in a paper I've found on the web suggests that actually you get some such bound as

|F| >= exp(-17280) / p^(8640+1080 log p)

where those numbers could doubtless be reduced by being less sloppy than I was, but probably not hugely reduced.

So, that would lead to a contradiction when

                               2^-p p^(8640+1080 log p) < exp(-17280)
                               -p + 8640 log p + 1080 (log p)^2 < -17280
                               p - 8640 log p - 1080 (log p)^2 > 17280

which is true provided p >= 298000 or thereabouts.

So ... if I haven't botched the above in any way (which I probably have), you "only" need to check a few hundred thousand values of L. You'd do that in practice by calculating log 3 / log 2 with sufficient accuracy (plain ol' double precision should be fine) and looking to see how close to an integer you can get by multiplying it by an integer up to a few hundred thousand in size.

Gareth McCaughan

.sig under construc

Von: Gareth McCaughan gareth.mccaug...@pobox.com
Datum: 25 May 2004 00:30:14 +0100

I wrote:

> According to theorems mentioned at the start of chapter 3 of Baker's "Transcendental Number Theory", the following is true.

> So ... if I haven't botched the above in any way (which

> I probably have), you "only" need to check a few hundred

> thousand values of L. You'd do that in practice by calculating

> log 3 / log 2 with sufficient accuracy (plain ol' double

> precision should be fine) and looking to see how close to

> an integer you can get by multiplying it by an integer

> up to a few hundred thousand in size.

I just received some e-mail from a friend of mine who knows much more about number theory than I do, observing that (1) it's rather well known (to those who know such things, I suppose) that the 3n+1 conjecture itself follows from some sort of bounds on the approximability of log 3 / log 2 by rationals, and (2) that the required bounds are much tighter than those obtainable by methods of the sort I mentioned. So if Gottfried Helms's conjecture is strong enough to do much for the 3n+1 conjecture (I'm not sure what a "primitive loop" is, I'm afraid) then the argument I sketched probably has some big holes in it.

Contrariwise, if I've somehow managed to break my perfect record of never posting anything to sci.math.research without at least one serious mistake, then Gottfried's conjecture probably doesn't imply anything very exciting about the Collatz conjecture. It's after midnight local time and I should be in bed, so I shan't attempt to determine which of the three possibilities - the third being that Gottfried and I are both right, and that Gottfried has found a way to make progress on Collatz with weaker inequalities than others have obtained -- is the truth. I'm just sounding a note of caution. :-)

Gareth McCaughan

sig under construc

Von: Gottfried Helms he...@uni-kassel.de
Datum: Tue, 25 May 2004 18:17:31 +0200

Gareth McCaughan schrieb::

> I wrote:

>>According to theorems mentioned at the start of chapter 3

>>of Baker's "Transcendental Number Theory", the following is

>>true.

> ..

>>So ... if I haven't botched the above in any way (which

>>I probably have), you "only" need to check a few hundred

>>thousand values of L. You'd do that in practice by calculating

>>log 3 / log 2 with sufficient accuracy (plain ol' double

>>precision should be fine) and looking to see how close to

>>an integer you can get by multiplying it by an integer

>>up to a few hundred thousand in size.

> I just received some e-mail from a friend of mine who knows

> much more about number theory than I do, observing that

> (1) it's rather well known (to those who know such things,

> I suppose) that the 3n+1 conjecture itself follows from

> some sort of bounds on the approximability of log 3 / log 2

> by rationals, and (2) that the required bounds are much

> tighter than those obtainable by methods of the sort I

> mentioned. So if Gottfried Helms's conjecture is strong

> enough to do much for the 3n+1 conjecture (I'm not sure

> what a "primitive loop" is, I'm afraid) then the argument

> I sketched probably has some big holes in it. Contrariwise,

> if I've somehow managed to break my perfect record of

> never posting anything to sci.math.research without at

> least one serious mistake, then Gottfried's conjecture

> probably doesn't imply anything very exciting about the

> Collatz conjecture. It's after midnight local time and

> I should be in bed, so I shan't attempt to determine

> which of the three possibilities -- the third being

> that Gottfried and I are both right, and that Gottfried

> has found a way to make progress on Collatz with weaker

> inequalities than others have obtained -- is the truth.

> I'm just sounding a note of caution. :-)

Hmmm, the stated inequality results from a "primitive" loop, let me explain that.

---------------------

Assume the transformation T on an odd x with the parameter A

y= T(x;A)

being

y= (3x+1)/2^A

where A is the highest exponent keeping y integral (which is actually only a short form for multiple steps of the collatz-transformation, collecting all subsequent x/2 - operations) and allowing short form for recursive notation:

z= T(y;B) = T(T(x;A);B) = T(x;A,B)

then a loop of, for instance, length 2 occurs, if

z = T(x;A,B) = x

------------------------------------------

The occuring equations are under investigation in some articles, that I've come across (mostly via internet), and are obviously difficult to handle, but of high general interest, as I learned this way.

My first approach was to deal with any type of loop, the general form

x = T(x;A,B,C,D,..M)

= T(x;A,B,C,D,...,M,A,B,C,...M)

= T(x;A,B,C...)...

for what I've got some nice results, but still not in the form of a general formulation, which could, for instance, easily been transferred to 5x+1 and other classes of the problem.

So I decided, first to investigate a somehow "primitive" loop.

I assumed most primitive loop (besides the trivial one, which is in this notation 1 = T(1;2) = T(1;2,2) = T(1;2,2,2,2,2,2,...) ) for my purposes the type of loop, which starts with one or more ascending steps, and then descends in one step. These are the assumed loops of the form

x = T(x;1,1,1,1,...,1,A)

where immediately strong restrictions apply on A.

One reason why I assumed that type as somehow primitive, is, that any eventual loop can be expressed as a collection of ascending steps between descending steps, if the length 0 is allowed.

So an arbitrary transformation, for instance

y = T(x;1,1,3,1,4,2,1,1,3)

can be segmented in

y = T( T(T(T(T(x;1,1,3);1,4);2);1,1,3)

and eventually I can use my tools, that I developed in the analysis of the "primitive" loop.

-------------------------------------------------------------

If I analyse the transformation of length N

z = T(x;1,1,1,1,...,1,A) where the number of ones is denoted as "L",

and check, whether it is ever possible, that we find a solution in integers, where z equals x, I come to an expression of the right hand side of my inequality, that I stated her in my previous postings, which also reflects an *additional* restriction.

With an arbitray 3-step-transformation, x' = T(x;A,B,C) with the length N=3, where x' should equal x (thus realizing a loop) with x,y,z, the intermediate values of each transformation, we can formulate a strong restriction on the exponents A,B,C:

since y = (3x+1)/2^A , z = (3y+1)/2^B , x'=(3z+1)/2^C and x=x' assumed (to form a loop), we can write their product as

           (3x+1) (3y+1) (3z+1)
     xyz = ---------------------
             2^(A+B+C)

Rearranging this we have:

                 (3x+1) (3y+1) (3z+1)            1          1          1
    2^(A+B+C) = ---------------------   = ( 3 + ---) ( 3 + ---) ( 3 + ---)
                  x   * y * z                   x          y          z

and obviously the range for the rhs is 3^3 .. 4^3 , so the sum of the exponents S=A+B+C must be an integer, which makes 2^S falling in between this range.

     3^N   <   2^S <= 4^N    (this is valid for any length N of assumed loop)
                              (for generalizations like the 5x+1-problem this
                               is equivalently 5^N < 2^S < 6^N)

Even more, this equation shows without any lengthy proof, that whenever the sum S is in general 2*N, then *all* parentheses on the rhs must take their maximum, and this is 4 for each of them.

This restricts then all x,y,z to be 1 , which in turn restricts all A,B,C to be 2.

Result: if S = 2*N then x = T(x;A,B,C,D...) only if A=B=C=D=...=2 and x = 1

----------------

It also shows a widely unknown property of the loop-problem, that the values of x,y,z have *high bounds* - which is important, since often articles about the collatz-problem assume loops in "high number" areas, if they don't find a solution in small accessible values. That is definitely not true: the values of the members of an eventual loop are much restricted in values.

Since the trivial loop is not of interest, we only have to study the cases

2^S < 4^N

and since 2^S must be at least the next power of 2 after 3^N we have the inequality

powerceil2(3^N) <= 2^S < 4^N

Now from the expansion of the three transformations into explicit formulas we get possible S; and I observed, that they were *always* smaller than powerceil2(3^N) in my cases of primitive loops. The contributions here in sci.math.research , sci.math and by some private posts showed, that there is an *extremely* high likelihood, that this inequality never holds. However - that's still no proof, even not for this simple case.

----------------------------------------------------------

I think, I made the needed progress now by investigating some modular classes, which exhibited a useful, very simple structure for candidate numbers x and y.

The above form of the inequality, stated for a "primitive" loop of length N with L=N-1 ones and one exponent >1

x = T(x;1,1,1,1,1....1,C) with L ones, C>1 and x odd integer>1

This problem can be separated into two:

y = T(x;1,1,1,1,1,1...1) with L=N-1 ones ("iterated transformation")

z = T(y;C) where z should equal x

An iterated transformation like y=T(x;1,1,1,1,1....1) with L ones restricts x and y to a very specific modular structure. it comes out, that - with a free parameter i ranging of nonnegative odd integers - x and y *must* have a very simple structure depending on the length of the requested iterated transformation:

x = i * 2 * 2^L -1
y = i * 2 * 3^L -1

thus

                          3* ( i * 2 * 3^L -1 ) +1
     z = (3y+1)/2^C   = -------------------------
                                2^C

and if z = x

                            3* ( i*2*3^L -1 ) +1
     x = i*2*2^L -1    = ----------------------
                                   2^C

After rearranging I come to the equation

                          i*3^N -1
              2^C = 2 * -------------
                          i*2^N -1

and with S = C + 1*L the stated inequality must hold:

                                                 i*3^N -1
    powerceil(3^N) <= 2^S = 2^(C+L) = 2^L * 2 * --------- < 4^N
                                                 i*2^N -1

If this inequality does not hold, then such a type of loop cannot exist - irrespectively of any assumend length.

-------------------------------------------------------

I stated this inequality for the case i=1 . For growing i the middle part of the inequality is better written like the following

                           3^N - 1/i
                     2^N * ---------
                           2^N - 1/i

and this converges to 3^N, which is definitevely smaller than the lhs:

for i->oo the inequality

powerceil2(3^N) <= 3^N

is obviously false.

So the case with i=1 was the most critical case, and I accept the information and learned the arguments for the extremely likelihood, that this inequality cannnot be satisfied for any parameter L and C but which is still not *proven*....

------------------------------------------------------------------

If that's solved, then at least a "primitive" loop can be actually negated - which is surely no great step in the whole loop-problem or even the general collatz problem - but... it's a start.

Therefore I'm also more interested in extensible proofs than in min/max-estimations for separate cases, if they cannot be generalized to other collatz-type-problems.

...

Unfortunately, a disproof of this type of collatz-loops is not conversely saying something on the above inequality, insofar it concerns unproved assumtions about the 2-log of 3 and the like, what you and others had derived here - that's bad luck. But I've got the impression, that some of my equations in this context could be helpful for progress even in that regard. I'll post them, if I've time these days.

Hope I answered the questions, that you rose in your post, even if I had difficulties to really follow your four segments today... :-)

Regards -
Gottfried Helms

Von: Gottfried Helms he...@uni-kassel.de
Datum: Tue, 25 May 2004 18:26:36 +0200

Gareth McCaughan schrieb::

> According to theorems mentioned at the start of chapter 3 of Baker's "Transcendental Number Theory", the following is true.
(...)

Hi Gareth -

that's a very interesting material, thank you (hope, I'll ever learn to apply that myself). I'll study it in more detail next days, since I'm guessing another connection to that field here, where my derivations on number-structure possibly could give additional information - or at least some more insight - I'll post it another day.

For an explanation for the origin of my question please see my other post.

Regards -
Gottfried Helms

Von: stei...@math.bgsu.edu (Ray Steiner)
Datum: 1 Jun 2004 10:48:53 -0700

Gottfried Helms <he...@uni-kassel.de> wrote in message <news:c94mv1$jl8$05$1@news.t-online.com>...

> Am 24.05.04 01:00 schrieb Gareth McCaughan:
>> Gottfried Helms <he...@uni-kassel.de> writes:

(…)

I proved the nonexistence of a circuit in the 3x+1 problem in 1977.

Is this what a "primitive cycle" actually is? A circuit is a cycle with one rise and one fall.

In fact, B. deWeger has recently shown that there is no cycle in the 3x+1 rproblem with less than 69 rises and falls in it. I can actually extend this to 70 and 71 rises and falls with Rhin's inequality which I mentioned in an earlier post.

Regards,
Ray Steiner

Von: Gottfried Helms he...@uni-kassel.de
Datum: Wed, 02 Jun 2004 17:54:37 +0200

Am 01.06.04 19:48 schrieb Ray Steiner:

> (…)

Hmm, that's interesting. I called it a "primitive", if there are N-1 steps ascending and 1 step descending, like it is in (7->11->17) -> 13 which, written as an transfer only noting the occuring exponents-of-2

13 = T(7;1,1,4)

My question was

"is there any solution in integers x,N,A with
x = T(x;1,1,1,1...1,A) with the 1 (N-1)-times occuring
establishing an N-Step-Loop

I found this very tight relation to the 3^N - 2^N properties, thus my question here.

The case of only one-raise-one-fall, if that means

x = T(x;1,A)

would then just be a special case of my question and can be proven by enumeration or even modular arithmetic.

But I would like to know, how you accessed the problem of this specific of rises&falls? I have a formula, how you can disprove a circle of *any* finite combination of raises&falls in finite number of tests, let say 100 raises&falls by a number Z of tests, where Z is a combinatorical function of about 42, which I'm bounding down by optimizing my formulas.

My attempt was to generalize these formulas to *unlimited* Z.

The "primitive" Loop is the most simple structure of that general problem of unlimited length, and has very tight and handy relations to the (3/2)^N - structure and that of frac( (3/2)^N), which I'm currently investigating.

---------------------------

Concerning your reference to deWegner:

His literature looks interesting, especially those with the focus on binomials: that was the next idea, that I wanted to step in. As I pointed out in a previor post the related problem can be represented using a rep-unit-form and the question, whether 3^n-1 div 2^N can ever be a repunit base a certain power of 2^P with p reasonably greater than N (don't have it at hand just now). I'm currently studying, what the binomial- expansion of 3^N = (2+1)^N explains for that problem.

Just have seen your reference to Rhin: could you point to a reference?

Regards -
Gottfried Helms

Von: stei...@math.bgsu.edu (Ray Steiner)
Datum: 1 Jun 2004 10:41:08 -0700

(…)

There is a paper by Georges Rhin(1987) in which he proves that

|p log 2 - q log 3| > H^(-13.3),

where

H = max(p,q) and
H > 2.

After that, just check the convergents of log-2(3).

Regards,
Ray Steiner

1. A large-scale view into the distance of 3N and the next perfect power of 2

1.1. The problem

1.2. The function f(N) under consideration and the hullcurve of moving minima

1.3. First impression and the idea of a hullcurve (or envelope)

1.4. The lower envelope for f(N)

1.5. More values and another hullcurve

2. Appendix

2.1. Data for graph of envelope:

2.2. Table 2: upper bound for the minimal member "a" of an assumed general cycle of length N (also based on the assumtion of maximal density of set of members)

2.3. Envelope for more coordinates (1600 coordinates up to N=10250)

2.4. Envelopes for other problem-configuration: 2S/3N, 2S/5N , 2S/11N

2.5. An earlier discussion in sci.math research (may 2004)

1. A large-scale view into the distance of 3^N and the next perfect power of 2

2.3. Envelope for more coordinates (1600 coordinates up to N=10²⁵⁰)

2.4. Envelopes for other problem-configuration: 2^S/3^N, 2^S/5^N , 2^S/11^N