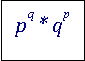|
|
||||
|
Problems and heuristics using infinite combinatorical matrices
The initital clue was here the analysis of the Pascalmatrix as a tool for the computation of the Bernoulli-numbers. See the first article below. This extended then in the play- and joyful discovery of many properties like its remarkable matrix-logarithm, of its properties when taken as operator but also that of the surprising simple form of its powers and so on. After that the relations to many other matrices with numbertheoretic/combinatorial coefficients popped up so that I started a compilation of descriptions for such matrices and their relations. The detailed list is in a subdirectory of this list of articles here. Very naturally one could also discover the matrix-summation methods for divergent series, like Cesaro-, Euler and Noerlund summation - all in the same framework of triangular infinite matrices with that, now familiar, coefficients. Finding, that the Pascalmatrix is also a matrixoperator for the map xp -> (x+1)p it is natural to study its matrix powers which just reflect such iterated maps - so this gives an interesting entrance into the functional composition and iteration of many other matrices which can serve also as matrixoperator. Only after I'd done some intense studies of their properties I could relate that all to the names "Bell matrix" and "Carleman matrix" under which exactly that had already been studied before - however seemingly only well known to a fairly small community. The playing around with functional iteration with that matrices give then the completely natural access to the iteration of the exponential function and the problem of tetration. Because of the amount of material I've left that in a subdirectory "tetration".
|
|
||||
|
|
|
||||
|
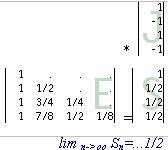
Bernoulli-numbers and the Beauty of the Pascal-matrix... The binomial- or Pascal-matrix occurs as very special entity in the zoo of number-theoretic creatures. It can serve as a defining tool for the Bernoulli-numbers; and looking at this one is led to the concept of eigenvectors; the construction of a new matrix (Gp and Gm) from the complete set of eigenvectors leads then to the Faulhaber-formulae, or, better known, to the integrals of the Bernoulli-polynomials and their use for the very old and venerable problem of summing of like powers of natural numbers. Investigating things further it exhibits a very basic matrix-logarithm; the G-matrices have themselves a nice eigen-decomposition into the matrices of Stirling-numbers... Just all my initial fiddlings from about 2006:
|
|
||||
|
... and a toolbox filled with numbertheoretical matrices. A subsequent collection of articles about further combinatorical matrices (Stirling numbers, Vandermondematrix and related/derived from that) which are in relation to the Pascalmatrix and the new Gp and Gm-matrixes. When I evaluated these matrices, more and more interesting properties popped up and very interesting connections to fields of number-theory occured. This introduced then a search for systematics by exploring matrix relations and reading literature. The main collection of articles is now a compilation of these properties (some are "exotic") as manuscripts, which I am refining step by step with references, proofs and links as they'll occur to me. The whole project is called "Identities involving binomial-coefficients, Bernoulli- and Stirlingnumbers" Keywords: Pascalmatrix, Stirlingnumbers, Eulerian numbers, Bernoulli numbers, Zetamatrix, infinite matrices, combinatorical matrices
I was later undertaking a complete restructuring and editing of all the above articles but was interrupted and should again review things. However, the new version may be found here. Note, that the project-related links in the articles partly still point to the old versions, so you should always return to the html-projectindex. Also they are not intensely reviewed, so for confusion, which possibly may have occured in the restructuring and may have survived I have to plea for patience...
… unfortunately the study of the iterated exponentials (see tetration) consumes almost all of my time, so I couldn't update and finish this project… Hope I can come back to this soon (Jan 2009) Keywords: Pascalmatrix, Stirlingnumbers, Eulerian numbers, Bernoulli numbers, Zetamatrix, infinite matrices, combinatorical matrices
|
|
||||
|
|
|
||||
|
Some more special properties of the Pascalmatrix
and a step into The analysis of the binomial/Pascal matrix is extended and more systematized. Additionally a matrix-representation of common summation procedures is investigated. Since I mainly deal with the binomial-matrix, this is almost all about variants of the Euler-summation. The article is in the state of a draft; I'm currently studying the heuristics and assumtions in more details and shall provide more links to literature and online-resources. See pmatrix.pdf Keywords: Euler summation, divergent series, matrix summation method
|
|
||||
|
Summing of like powers - solved using the
Pascalmatrix, finding the ZETA-matrix I re-accessed this old and venerable problem using my concept of expressing things in "operator-matrices" (which are, as I've learned much later, actually the "Bell"/ "Carleman"-matrices) more systematically than in my first encounter with the Pascal-matrix and extend the earlier found Gp and Gm matrices to the full ZETA-matrix (which I could also use to re-express the Euler-MacLaurin-formula in the same matrix-rationale, see article below). Here I discuss a derivation simply by using the geometric series (Neumann series) of the Pascalmatrix, which leads first to a summing-operator for alternating sums of like powers and after that also to the non-alternating sums. The derivation here involves the basic definition of the values of the (Dirichlet's) eta- and the zeta-function, thus leads from eta/zeta-values to the eta/Bernoulli-numbers as a special case. see: Sums-of-like-powers Keywords: Sum of like powers, Bernoulli polynomials, Faulhaber polynomials, Zeta-matrix
|
|
||||
Properties of the Bell-numbers, generalization to fractional indices and (divergent) sumsGetting more and more used to the concept of divergent summation is was a challenge to try this with the Bell-numbers and because they are in tight connection with them, the Stirling numbers 2nd kind. I determined polynomial expressions for the generalized Bell-numbers which allow to interpolate the column-index. See (Generalized) Bell numbers and their sums Keywords: generalized Bell numbers, divergent summation, Stirling numbers second kind
|
r'th Bellnumber Br(s) [of (fractional) order s]
|
||||
Euler-MacLaurin-summation formula by ZETA-matrixThe Euler-MacLaurin summation formula is a classic and powerful form of representation for the sum of a function at consecutive arguments. After I'd found the ZETA-matrix as representation for the integrals of the Bernoulli-polynomials I got aware that we deal with the same entities here and found the Euler-MacLaurin-summation formula as a simple reordering of summation when the ZETA-matrix was again used. See Euler MacLaurin by ZETA-matrix Keywords: Euler-MacLaurin formula, Bernoulli polynomials, Zeta-matrix
|
|
||||
|
A matrix-method for divergent summation using the matrix of Eulerian numbers The Eulerian numbers are known to be interesting creatures in the combinatorics, and can also be found in the analysis of the problem of summing of like powers. The factorially rowscaled matrix of Eulerian numbers can even give a summation method for divergent series which is comparable with the Borel-summation insofar as it can sum not only the alternating geometric series of any order but even the alternating hypergeometric series 0!-1!+2!-3!+...-+... for which L. Euler had proposed the first meaningful result. That summation-method resulted from intense selfstudy of that matrix and seems to be a regular method even although it does not use the "rowfinite" version. The first discussion of that matrix and an introduction into the summation method see Eulerian matrix A further indepth study of the remaining non-summable series gave more interesting results, for instance how does the summation method transform the given series (even if cannot finally assign a sum): for the divergent nonalternating geometric as well as for the divergent nonalternating Dirichlet-/Zeta-series. Keywords: Eulerian numbers, matrix summation method, divergent series
|
|
||||
|
|
|
||||
|
Tetration and iteration of functions using matrix-operators - a subdirectory Some technical articles, mostly workshop-like material about tetration. When studying the "numbertheoretical matrices" I came across the matrices of Stirlingnumbers as matrix-operators/Carlemanmatrices for the map x -> exp(x)-1 resp. x-> log(1+x) and asked, what I would find, if I use their powers (and series of powers) like I did with the Pascalmatrix for the problem of summing of like powers (which had led to some nice insights into bernoulli-numbers, zeta/eta-function and even series of zetas/etas, see there). The result is "iterating analytic functions" (having powerseries) where this is possible and the generalizing to fractional iteration for maps of x->bx resp. x->tx - 1. This was already seriously considered by Goldbach, Lambert and Euler, and in the late 19th and the whole 20th century this was developed up to the problem of fractional iteration, where some aspects are still unsolved. Enter the "hellgate to the powerseries of tetration " Keywords: Tetration, Powertower, functional iteration, powertowerseries, halfiterate
|
|
||||
|
|
|
||||
|
Exponential diophantine problems
The residues of powers modulo some prime, the inherent patterns and then the "little Fermat's theorem" have been very attracting for me in the beginning of my number theoretical couriosity. One of the immediate attractions next was the Collatz-problem (or 3x+1 problem) for which I've invested many monthes of my life... This is since then the base for all of my studies in exponential diophantine problems: the famous "last unsolved problem of Fermat (FLT)" (solved 1996 by A. Wiles), the Catalan-problem, the question of Mersennenumbers and the finiteness of the set of Mersenneprimes and the study of primality-tests like the Lucas-Lehmer-Mersenne test, and that of cyclotomic polynomials and high Fermatquotients and many others of this type. It indicated, that it might be helpful to install first an explicite set of standard tools for the handling of such problems, thus my treatize on "cyclic subgroups".
|
|
||||
|
Mersenne numbers, cyclotomic polynomials and primefactorization By analysis of the problem of Mersenne-primes it is natural to generalize the question to the cyclotomic functions/polynomials. What I did here was analyzing the primefactorization of Mersenne-numbers and cyclotomic functions, finding this way an heuristic approach to the concept of cyclic multiplicative (sub)groups modulo a prime. This concept and an adapted way of analytical expression allows then to express and analyze more general exponential diophantine problems like Catalan's and Fermat's problems; the latter can for instance be focused to the question of solvability in terms of a generalized Wieferich-prime-concept which was done by Arthur Wieferich in the early 20'th century. See: cyclic subgroups
|
|
||||
|
Wieferich-primes and Fermat-quotients Originally I was interested in the so-called Wieferich-primes w, where 2w-1 = 1 (mod w2), (the two known cases w=1093 and w=3511) . That we know only two of such w means that exponents greater than 1 in that relation (which is due to Fermat's little theorem) seem to be really exceptional cases. The concept of fermat-quotients generalize this to other bases than 2 and to other exponents of the base of the modulus. I found some discussions about fermat-quotients in internet-articles; I found some system for fermat-quotients and also provide some "exotic" examples of high exponents. For more information for the interested reader I prepared a "directory" for further references. Keywords: Wieferich primenumbers, Fermatquotients
|
|
||||
|
The Lucas-Lehmer test for Mersenne numbers - revisited
in the view The Lucas-Lehmer test for the primality of Mersenne-numbers is an iterative procedure. In the context of my exercises with fractional functional iteration I found it a very natural candidate for the study. Surprisingly one result is the discovery of the "LL-constant", which allows to determine the primality of m=2n-1 just by testing LL(m+1) = 0 (mod m) . Unfortunately this is only of recreational value; we need about m digits of LL when we test m for primality... See "Lucas Lehmer"
|
|
||||
|
|
|
||||
|
Collatz-(3x+1)-problem The Collatz-problem was a main subject for me for several years ago. Sometimes I felt to succeed, but was always lacking the final proof. Thus I reduced my study to the smaller question of existence of cycles in the collatz-transformation. I decided for a special notational framework focusing the exponents/the structure of a transformation rather than the elements and found some nice properties. However, although this approach allows to disprove some cycles, the general cycle of arbitrary length was still too complex for a definitive result. Then the existence of cycles of arbitrary length but in the simplest possible form (I called them "primitive loop", in use was also the name "1-cycle" or "circuit") was investigated in detail. This lead to an intimate relation of approximability of powers of 2 to powers of 3, so this seems to be the main and the crucial problem at the heart of the Collatz-cycle-question. For instance, investigating this property one finds a connection to the problem of z-numbers (studied by Kurt Mahler) and even (according to E. Weissstein at mathworld) to an unsolved detail in the Waring-problem – a connection that seems not to be widely known. The "primitive collatz-loop" was already disproved by Ray Steiner ("circuit") in 1978, and some concatenations (on the way to the general cycle) had already been disproven by Simons/de Weger in 2000 and 2002. Not knowing their results beforehand I came to very similar formulae, but stuck at the problem of proving the nonexistence of cycles by them. See for an intro for amateurs: see: Cycles in the Collatz(pdf) (a slightly compacted version) See also here: Collatz loops (html) . (The oldest version, in ugly ascii-art but which I like for historical reasons.) Not all material from this is taken to the pdf-version, so especially the section on pictures/graphs is still a nice resource.
Keywords: Collatz-problem, Collatz-conjecture, 3x+1, 3n+1, Collatz cycles
|
|
||||
|
Approximation of perfect powers of 3 to perfect powers of 2 Derived from the Collatz-loop-discussion there is a small discussion of approximation of perfect powers of 2 to such of 3, say 2S to 3N . See approximation of 2^S to 3^N
|
|
||||
|
|
|
||||
|
Asymptotic density of primefactors in the Eulerian product of the zeta-function The Eulerian product-representation for the zeta-function has in the denominator an interesting expression - interesting: after one has generally become familiar with the question of primefactors of expressions like an-1. The denominator of the Eulerian product is now an infininite product of such expressions and where all a are themselves prime-factors. So I looked at the relative frequency of the primefactors q of the denominator when truncated to, say, w terms : (2n-1)(3n-1)(5n-1)...(prime(w)n-1) with the idea to let w grow without bounds. Every factor in that product contains a prime base a as its characterizing element, but none of them is prime. If we denote one prime factor q and count for a given w and given n all its occurences in the w separate product-terms as sum sq,n,w then one can find some expression for the relative frequency rq,n,w = sq,n,w/w of the primefactors q depending on w for each power n. See "Prime Density" The heuristical formula was later confirmed in a thread in MO. See (MO) the relative count of the primefactors(...)
|
|
||||
|
|
|
||||
|
Other musings and mathematical recreations
Just some other discussions which evolved mostly in the time when I studied functional iteration and any attracting exotic number theoretic idea...
|
|
||||
Factorizing of exp-function: the "Dream of a Sequence""Dream of a sequence" – when I played with the question, whether it would be possible to express powerseries, for instance the exponential-function, by an infinite product I found a nice solution some years ago. Recently a correspondent, who has been stumbled into the same question, asked me for a comment, and I looked again at the problem. This time I recognized that the found coefficients contain a beautiful sequence of numbers – just "a dream of a sequence". Keywords: Exponential function, factorizing
|
|
||||
|
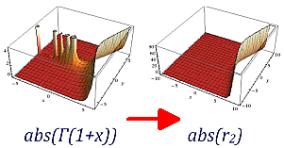
"Uncompleting" the Gamma-function I was surprised by the seemingly simple pattern of the taylor-series for the gamma-function: the coefficients tend to 1 very fast. Well – if it is partly so simple: why not invent a separation into one series, which has a closed-form expression (like the geometric series) and into another, residual series, but which is better converging? A short discussion using two different replacements. The latter rediscovers the incomplete gamma and gives thus a nice heuristic/intuitive interpretation. A not-yet-finished contemplation is that of understanding the Gamma as iteration of another function and that of relating this to known concepts of fractional iterates. See "uncompleting the gamma" (current version: 08'2012) Keywords: Gamma function, incomplete gamma, zeta-function, Stieltjes numbers, gamma as functional iteration
|
|
||||
|
The inverse of this matrix M is the Null-matrix? In a discussion in the mathematical exchange on MSE I was triggered to look at the problem with an proposed attempt to define the inverse of an infinite matrix. The question was whether such an inverse can meaningfully be defined when the inverses of increasing finite size are observed and if they (seem to) converge to a fixed pattern of entries. To understand and then to approach the problem I tried a special, but simple (Vandermonde-like) matrix M to get its supposedly formal reciprocal W ... and that inverses with increasing finite size... ... seemed to come out to be completely near zero. I discussed this with the help of the L D U-matrix-decomposition. The L-D-U-components are triangular and have for any finite truncation the same pattern of entries. Also they have well defined triangular inverses which are also always invertible and thus have a natural generalization to the case of infinite size. The formal dot-product, or better: the analytical description of the formal dot-products gave now an infinite, and highly nontrivial, set of identities (involving the Stirling numbers 1st kind) where the first dozens of empirically tested formulae indeed evaluated to zero. I could also decypher the much likely correct analytical expression for the involved dot-products by the involved not too exotic patterns of numbers. A general formula for each entry of the resulting infinite matrix W is given, but I did not get a general proof yet, that indeed all formulae come out to be zero. See "infinite Nullmatrix as inverse of M" Just recently ( Aug 2014) a contributor in MO provided a proof which can easily be usded in an induction. See (MO) an infinite set of identities are they all zero?
|
|
||||
|
Sums of like powers of logarithms - playing with indefinite summation In various contexts I arrived at the question of series of logarithms like log(2)-log(3)+log(4)-...+... Such series can be summed as far as we allow methods of divergent summation, for instance Cesaro or Euler-summation of appropriate order suffices. A simple rationale for the sum of the non-alternating series of logarithms might then be the regularizations of the derivative of the zeta(s) at s=0. However, I tried to examine my older method (with which I'd already found the sums-of-like powers using the Pascal-matrix) to apply this now to the related problem of like powers of logarithms - and in the similar fashion as the Faulhaber-/Bernoulli-solution works for the sums of like powers. I could define a meaningful infinite set of coefficients, which allow to transfer the Bernoulli's ansatz of summing ap+(a+1)p+(a+2)p+...+bp into that of summing (log(a))p+(log(a+1))p+(log(a+2))p+...+log(b)p. The difference to the Bernoulli-solution is however, that we do not get polynomials of p+1'th order but power series. The result is presented as a matrix, which contains the coefficients for the required powerseries, and prominently that for the lngamma(x) for the sum using exponent p=1. See "Bernoulli for Log Sums" A recent "rediscovery" of the idea of sums of like powers of logarithms appeared in the Q&A-forum MSE see (MSE) formula for sum of logarithms ln(n)m
|
|
||||
|
Integer relations between acosh()-values ... finding a fractionally iterable family of polynomials By accident one can find that the transcendental function acosh(x) at different arguments can have integer ratios. This extends also to asinh(x), acos(x) and asin(x) as well. Experimenting with this was a fun; and also leaded to a well known case of a family of polynomials, which occur by iteration and allow even a natural solution for the (in general very difficult or even unsolvable) problem of fractional iteration. See "acosh() integer ratios"
|
|
||||
|
|
|
||||
|
Continued fractions |
|
||||
|
Continued fractions with powers of e Triggered by a question in a mathematical discussion group concerning continued fractions of powers of e (euler constant, base of natural logarithm) I deduced a pretty general formula for expressing powers of e in terms of very regular non-regular continued fractions. The result came out to be known in terms of continued fractions of tan(x). See: (article temporarily retracted) For e-1 there is a nice "generalized continued fraction" with a very simple pattern in its coefficients. I asked: what if the pattern remains, and only the offset is changed? We find rational compositions of e but surprisingly for some general relation of the offsets we seem to get rational values for that infinite continued fractions! See: GenContFrac RationalValues
|
|
||||
|
Continued fractions – generalization Three ideas composed together: a) the well known matrix-multiplication scheme for convergents of continued fractions leads to an eigenvalue-view into that matter. b) That eigenvalue-view reflects then the occurence of periodic continued-fraction-parameters when square roots of rational numbers are irrational. c) Now why can't we find periodic parameters for higher roots? The eigenvalue-idea is then applied to approriate dimensional matrices, for cube-roots use 3x3-matrices and so on. Now, if one has a representation of a periodic integer matrix-multiplication - can the rational approximation of an algebraic number be better than 1/q2 ? See: (article not yet ready)
|
|
||||
|
|
|
||||
|
Other uncategorized material
One can even have/make fun in the math community
|
|
||||
|
Sums of like powers - a very basic hobby treatize with which I rediscovered the Eulerian numbers An elementary approach discussing properties of sums of like powers, which *should* be reworked. But since they were my first number-theoretical experiences in that area, I keep them alive... :-) You'll find the use of the Euler-triangle here
|
|
||||
|
|
|
||||
|
Fun in sci.math - "An unknown document of P.d.Fermat discovered" (03'2002) The usenet-newsgroup sci.math is well known for the many enthusiastic Fermatists; one of the greatest contributors among them being J.S.H., who recently promoted his revolutionary concept of math-of-objects (or "object orientated math"). So it was obvious that this newsgroup would be the best place to announce the sensational finding of an unknown document, most likely a formula with which the great french mathematical amateur Pierre de Fermat set himself an obelisk. I announced this finding in march, 2002. Enthusiastic reactions in the readers' community showed that this was really a hit.
|
|