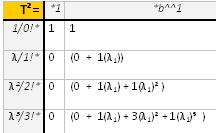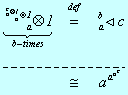|
|
|
Here I present some material about tetration. Most of it is in manuscript-state as handouts for some interested collaborators, some of it is meant as basic introduction and review of my own learning. The explorative articles do not pretend to be more than more or less heuristical findings meant as impulse for further investigation. However: the more I read in related literature I see, that many of my ideas and procedures are already known. New aspects, and seemingly original ideas, seem to be
· the consise systematic notation in a framework of pure matrix-formulae, · the inclusion of techniques of divergent summation · and the consideration of infinite series of powertowers.
Being an amateur in mathematics all of the following is explorative. The most needed enhancement is a systematic notation (and translation of the current notation), checks for ranges of applicability and proofs (as far as there are no proofs in the available research)
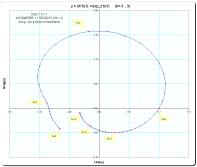
The picture at the right, by accident produced for the "characteristics"-article, may serve as icon from now: be warned when you engage in tetrational-powerseries:"the hellgate to tetrational powerseries"
|
|
|
Overview
Powertowers, with a base b and an initial value x are x, b^x, b^b^x, … . Often people assume x=1 and simply write 1, b, b^b, b^b^b,… and introduce a "height"-parameter to indicate the "height" of the powertower (I'lll use the letter h for this). One fairly common way to write this is b^^h. where b^^0=1 and b^^1=b. However, that notation isn't expressive enough in many circumstances. For instance it is a systematically interesting variant to use the decremented version b^x - 1 instead of b^x and work on the formal powerseries of this. The most flexible notation seems to be to use the name of a type of function, say exp(x)=e^x use a base-parameter as subscript, such that expb(x)= exp(ln(b)*x) = b^x and an iteration parameter like exp_b°h(x) where exp_b°0(x)=x and exp_b°h+1(x)= exp_b°h(exp_b(x)) For the interesting modification to the decremented exponentiation it was used to write dxp_b°h(x) in the tetration-forum. [see TForum] For the sake of compactness in the following articles I used "T-tetration" for powertowers b^...^b^b^x, thus Tb(x) = bx and Tb°h(x) the h'th iterate; and "U-tetration" for Ut(x) = tx –1, where if t is omitted, U-tetration denotes simply exp(x) – 1 or "dxpe°h(x)" . Unfortunately I was exploring the subject with little experience in the beginning so this is not consistent over all articles.
T-, U-tetration, different fixpoints and non-uniqueness-problem It may be helpful to understand, why in T-tetration I use the letter b for base, but in U-tetration the letter t: because (at least for integer height of iteration) we may replace a Tb-tetration by a Ut-tetration of another base t, where b=t1/t and it seems sensical to keep different letters to remind the reader of the fact of relation of two compatible bases. There is an interval on the real line for the bases b, where the powertower of infinite height still converges; this intervall was found by Euler and Goldbach and many other mathematicians later. It can best be described by the following. Assume b=t^(1/t), and u=ln(t). Then the range for convergence is –1<=u<=1 or exp(-1)<=t<=exp(1), and exp(-exp(1))<=b<=exp(exp(-1)) which is in numbers about 0.065988…<=b<=1.4446678….. To "arrive at convergence" when the function is infinitely iterated means that the limit-value is a "fixed-point" and also already Euler had showed that the fixpoint is just the value of the value t in the definition of b.
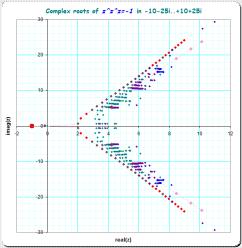
These t are thus fixpoints of the Tb-tetration. Bases where b is outside the interval exp(-exp(1))...exp(exp(-1)) have only complex fixpoints t, so this forces also the consideration of general (complex-based) U-tetration in a completely "natural" way. (See the article how to compute complex t, for which the corresponding base b is an arbitrary real number).
Unfortunately, the nice representation of Tb-tetration by Ut-tetration using fixpoint-shift leads to different solutions for fractional iteration, if different fixpoints are considered. There are infinitely many complex tk satsifying tk1/tk = b and it was shown, that for fractional iterates the different tk give different solutions. This is an open problem in the analysis of tetration and is one aspect of the unsolved "non-uniqueness"-problem in tetration.
Formal powerseries and matrix-operators All discussions here are based on the analysis of formal powerseries, and specifically of the powerseries for the exponential-function exp(x) and exp(x)-1. The needed manipulations of the formal powerseries, like squaring or iteration, are best and most concise expressed in matrix-format in connection with a Vandermonde-vector V(x), which reflects the powers of x for the evaluation of a formal powerseries; I call the occuring matrices "matrix-operators" acting on formal powerseries. (see "continuous functional iteration" for some basics of this) This is very useful: inversion/reversion of a formal powerseries is then simply expressed as inversion of the matrix-operator and we can enjoy very concise formulae for the derivations of new formulae. Moreover – once introduced, this matrix-formalism has its own benefit: if the matrices are triangular (as it is for U-tetration) not only integer powers represent integer iteration of the underlying function; but since also fractional powers are then well defined (using matrix-logarithm or eigensystem-decomposition) this allows a well defined representation of fractional powers of the underlying function and thus a smooth implementation (and analysis) of fractional iteration of such functions. The interested reader may consult the book of L. Comtet or related articles of Aldrovandi/Freitas, Berkolaiko and Woon or even the wikipedia at "Bell-matrix", where the basic matrix-concept and the relation to integer and fractional iteration was already developed. All that said is meant using formal powerseries and thus matrices of infinite size. For nontriangular matrices is is already non-trivial to define integer powers (which we do not really need since to compute the integer-height powertower is just iteration on the scalar value) but even more, the fractional power. While for the integer powers I found a representation in exact terms (as far as log and exp can be assumed as exact), for the fractional power we have only the logarithm, the diagonalization and the "exponential interpolation". But the exact entries of the component-matrices of the diagonalization / matrix-logarithm are not easy to determine and one solution (that of the "regular iteration") yields complex entries for real bases if b is outside the Euler-range and this introduces problems which I was not able to solve yet. So a simple/naïve approach is to study the diagonalization of the truncated matrix-operators, say to the size of 32x32 or 64x64 if possible. This provides then an approximation to fractional powers of the matrix-operator and from this to fractional iteration which I call "polynomial interpolation". We can get meaningful approximations up to 10 digits or so by this and for the cases of b outside the Euler-range this gives concurrent (and possibly more realistic) estimates for the fractional iteration of exponentiation.(See the "4 interpolations"-article).
Divergence/zero-convergence-radius of powerseries for fractional iterates While a solution for the coefficients of a half-iterate of a powerseries without constant term can easily be determined, another problem occurs with the computation of the value of that powerseries: for fractional iterates they seem to have convergence-radius 0. and thus no solution for the fractional iteration of –for instance– exp(x)-1 is possbible. This is equivalent to the expression, that the absolute values of the coefficients increase with a rate higher than geometric order, the quotient of two consecutive coefficients increases with the index. Thus these coefficients dominate their associated powers of x (however small the absolute value of an assumed x is) - the powerseries will eventually diverge and thus convergence-radius wrt x is zero. In principle there is one possibility to overcome that limitation of divergence in the powerseries by the concept of divergent summation like Cesaro, Euler or Borel-summation. However, that well established summation methods for divergent series are not "powerful" enough to give arbitrarily accurate approximations of such powerseries. I suspect, that even Borel-summation is not powerful enough for these type of series. We can assign a value to a series 0! –1! + 2! – ... + ... via Borel-summation and may even be successful for a powerseries f(x) = 0! –1! x + 2! x2 – ... + ... (as shown by Euler) this way for some range of x The powerseries for fractional iterates seem to have even stronger growing coefficients. So far we can only give best approximations for such values, and it is an open problem to find one valid summation-procedure for these power series. I'm experimenting with some extensions based on the principle of Euler-summation/Euler-transform/Nörlund-summation, with some suggestive (but not finally proved) success yet. An additional Stirling-transform seems to help remarkably, but to be no general solution alone. See the articles "zero radius(…)" and "characteristics" for more about this.
Iteration-series, other series of exponential-towers
An interesting aspect which I've not seen elsewhere so far (except one specific series considered by Ramanujan) is the question of series of exponentialtowers; a special interesting aspect is the possibility of a better definition of fractional iterates by such exponentialtower-series instead of powerseries – a more serious motivation than the pure explorative fun. For shortness of expression and for better generalizability I'll use the term "iteration-series" for this in the following. We know already a formula for fractional iterates using a binomial composition of the iteration-series [Comtet, Woon, TForum] but the relation to the powerseries-expression of the same problem is not yet clear wrt to the use of different fixpoint-shifts. The matrix-notation gives rise to series of matrices, which suggest surprising results. Some of them seem to generalize known numbertheoretical properties to series of "higher orders" (but the first naive approaches showed to be insufficient yet). The point is then, that – although we are thinking in terms of formal powerseries and are used to that "the question of convergence can be neglected" – we are confronted with the convergence-problem on a new level, let's call it "meta-level": the coefficients of the resulting powerseries are now themselves subject of infinite summation and this may introduce new, unexpected effects.
I discuss three types of series of exponentialtowers: of increasing consecutive integer height ("tetra-series", "iteration-series"), of same height but consecutive base ("tetra-eta-series") and of constant height, constant base but increasing power of the top-exponent ("tetra-geometric-series"). For the "tetra-eta-series" of height 2 a comparable result exists due to Ramanujan, but which is different from the result which I derived here. This calls for further investigation of my assumtions. For the alternating tetra-series there was an extended discussion in the newsgroup "sci.math.research" in 2007 which finally seemed to have confirmed my basic result for the alternating "tetra-series" by a concurring summation-method (Shanks-summation). For the "tetra-geometric-series" I proposed a conjecture but which came out to be erronuous; the matrix-based computations of the series to negative infinity and to positive infinity in the top-exponents seem to miss the result by some systematic error which I couldn't characterize yet.
A completely different view into "tetra-series" is the opposite question, whether a given function f(x) (having an invertible powerseries) can be expressed as iteration-series itself (alternating or nonalternating) of an iterable function g(x). It was interesting, that the representation of f(x) = log(1+x) as "iteration-series" of g(x) = (1+x)/exp(x)-1 gave a new(?), very good approximation method for the logarithm-function for small values of x.
One more general remark At various times/places I expressed a concern about the order of indexing of the iterated exponentiation. That concern did not yet dissolve; here I express it in a discussion-page in wikipedia(see the copy on my webspace)
|
|
|
Articles |
|
|
Continuous functional iteration A short basic treatise of integral and fractional iteration of functions, which are expressed as powerseries (formal powerseries). Perhaps the best introduction for the powerseries/matrix-approach as I use it for all my articles. Examples of the integral and fractional iteration of geometric series, the sine-series and the decremented exponential-series (U-tetration) are presented and discussed in a short introductory manner. I present a concise symbolic description for the coefficients of the U-tetration-powerseries based on diagonalization depending on x and height h. (26.1.2008 Vers 0801-12)
|
|
|
Diagonalization for triangular matrix-operators The powerseries for fractional iteration can easily and meaningfully be defined by fractional powers of matrix-operators/Bell-matrices. This requires matrix-logarithm or eigensystem-decomposition/diagonalization. The article Eigensystem-decomposition describes the diagonalization-procedure of the triangular matrix-operator Ut for the computation of iterates of tx-1. A short overview, code for Pari/GP and symbolic sample-coefficients. (10.9.2008)
|
|
|
Comparision of two methods for fractional iteration. Results of the diagonalization-method (which I proposed here in several articles and in the tetration-forum) are compared to the results when computed using the method of binomial-expansion (here: "BinEx"-method). The BinEx-method was known already to L. Comtet (references see below), applied and described also by S.C.Woon and others. It has the advantage, that it provides fractional iterates using only integer iterates of the original function – however combined with fractional binomials. But fractional binomials can be computed using the gamma-function, which can be computed for fractional arguments with arbitrary precision. So the BinEx-method has a certain charme. The discussion in the article suggests, that the methods give asymptotically identical results, but that the diagonalization gives a better result with less terms of the involved powerseries. See Diagonalization vs BinEx (05.12.2008)
|
|
|
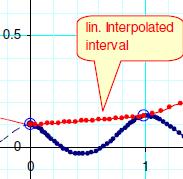
4 interpolations I discuss a couple of proposals for the interpolation to fractional iterates: the "reference version" regular tetration, a log-polar-based interpolation, then the "linear interpolation" as for instance suggested in the wikipedia-article and the "polynomial interpolation" as implemented by diagonalisation of the truncated matrix-operator/Bell-matrix. To have a nontrivial example I use the base b=4 which is outside the Euler-range and show the iteration-trajectories beginning at a complex starting point z0. The results are even qualitatively different, which asks for deeper study of the implications of each method. Unfortunately I could not yet include the interpolation based on the Cauchy-integral as presented by D. Kusnetzov and provided in the tetration-forum – this would be an important enhancement for this article. See ComparisionOfInterpolations (10.2.2011)
|
|
|
Exercises in iteration: Base b=0.04 A small base with negative logarithm of the fixpoint requires complex values for real fractional iterates. Here I discuss some observations. See Base 0.04 ( ------------- first version 08.06.2009)
|
|
|
Exercises in iteration: f(x) = 1/(1+x) I consider this case in terms of regular iteration based on the powerseries–representation. For the case of fractional iteration the function f(x), which has a constant term is replaced by g(x) without a constant term using fixpoint-shift, such that f(x) = g(x – x0) + x0 . g(x) can then regularly be fractionally iterated (the associated matrixoperator G is triangular, iterations are implemented via diagonalization). Then two other formulae are used, which allow the fractional iteration directly on the scalar values. Results of all methods seem to match, so the regular iteration using matrices and diagonalization seems to be justified here. But can we find another interpolation for fractional iteration, which, for instance allows equi-angularity in the trajectory of iterations? See Fractional iteration 1/(1+x) (upd ------------- first version 23.01.2009)
|
|
|
Exercises in iteration: f(x) = ln(2-exp(-x)) Another exercise triggered by a discussion on mathoverflow.net: See Fractional iteration ln(2-exp(-x))
|
|
|
Exercises in iteration: When is x^x^x=-1 ? (A question in MSE) Another exercise triggered by a discussion on math.stackexchange.com:
|
|
|
Pascal-matrix "tetrated" Since exponentiation is defined by a powerseries, we can define the exp-function for matrices as well. Here I do a short discussion of tetration using the Pascal-matrix as argument. So I ask: what is P^P, P^P^P and some related questions. Surprisingly, the tetrates of P give some sequences of numbers, which are meaningful in combinatorics (see references to OEIS). Also a "generalized" eigendecomposition for P is found. Surprisingly, even P^^inf can be defined in a meaningful way. See Matrix-tetrates (upd 16.1.2009 first version 26.12.2008)
|
|
|
Exact entries for integer iterates of the T-tetration matrix (Carleman/Bell-matrix) While the computation of the "decremented exponentiation" ("dxp(x)" or "U-tetration") uses a triangular matrix U, and thus powers, inversion, eigensystemdecomposition et al enjoy exact numeric (as far as we see log/exp as exact), the handling of the iteration of the non-decremented exponentiation (the common powertower, or "T-tetration") is much more difficult (and yet limited) to handle within the diagonalization-method because the matrix-operator T is an infinite sized square-matrix and powers of it involve the evaluation of infinite series for the computation of each entry of the matrix-power. Here I propose an analysis of these series and find, how to express them as finite composition of exponentials and logarithms, such that we have exact entries also for (integral) powers of the matrix-operator T. (27.09.2008)
|
|
|
Zero-radius of convergence for base e-tetration "No real iterate (f°h(x)) for f(x) = exp(x)-1 exists if h is non-integer". This statement in an article of Erdös/Jabotinsky triggered me to read also the source (I.N.Baker). Baker only says, "the radius of convergence is positive, iff h is integer". This is a less far reaching statement, since this allows possibly to determine meaningful values, if techniques of divergent summation are also considered and employed for evaluation of the occuring powerseries. A short treatise of this problem. Additional tables at U-Tetration tables (6.1.2008 Vers 1)
|
|
|
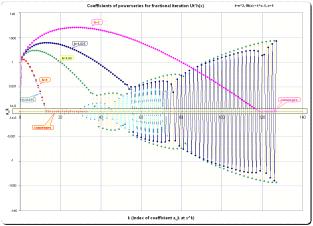
Characteristics of the powerseries for fractional iterates (U-Tetration). Here I give some plots to study the properties of their coefficients in a greater picture. 161 iterates from –2<=h<=2 are computed. Coefficients of some significant fractional heights together with the integral examples are graphed in curves and exhibit a certain pattern of divergence.
The goal with this is still to find a better suited general method for divergent summation of these series. Characteristics (html, some wide pictures) Printversion (pdf, reduced pictures) Also I produced some bitmaps using the whole set of computed coefficients to illustrate the more general behaviour. One of the plots exhibits the true nature of all this fiddling with tetrational powerseries:"the hellgate to tetrational powerseries"
|
|
|
Fractional iteration of a complex base My implementation of diagonalization and computation of Tb(x) using fixpoint-shift and application of Ut(x')" seems to have a bug, if complex bases are fractionally iterated, which I could not resolve yet. But the "exponential polynomial interpolation" (see below) seems to give now meaningful results. Please compare my results with concurring methods of computation. (18.07.2008 Ver 0807-1)
|
|
|
Exponential polynomial interpolation: The integer U-tetration (or dxp(x)) can be interpolated to continuous U-tetration using diagonalization or matrix-logarithm, depending on whether the bases t are equal or different to exp(1). I tried to express the interpolation of the powerseries for the increasing heights without the diagonalization approach, just in the same spirit as we would interpolate a list of values by polynomial interpolation – and found a solution in a variation using exponentials. The result is amazingly straightforward and simple and agrees perfectly with the diagonalization/matrix-logarithm-method. The article handles the problem of inversion of the vandermonde-matrix, which is required for matrix-based interpolation but is only possible for the case of finite dimension and the analoguous solution for the exponential polynomial interpolation. (14.7.2008 Vers 0807-1.1) I've seen that the q-analogues of factorials and binomials (q-Pascal-matrix) are essentially involved. (Updated 9.9.2009)
|
|
|
Tetration_function.pdf : How to find fixpoints for real bases b>e1/e |
|
|
Tetraseriesproblem: a description of the problem of incompatibility of summing the infinite alternating series of powertowers of increasing height ("Tetra-series"/"iteration series") using matrix-method and usual summation via partial sums of the series of towers. This is only a collection of ideas and descriptions; no solution is found yet. A more detailed introduction may be the article 10_4_Powertower.pdf below, where this inconsistency does not occur. (30.12.2007 Vers 6)
|
|
|
Older articles, most need review (!) The articles in this section result from my first encounters with the problem of iterated exponentiation and contain early heuristics. Also conclusions/conjectures were made, some are not valid when investigated later, or not valid in their generalizations. So the articles need be rewritten in the light of my later experiences and insights. However, the basic ideas are still interesting and introductions especially into the area of series of powertowers. And the generalized conjectures may even be worth to be corrected and restated for their relations to properties of non-tetration-powerseries.
|
|
|
Series of powertowers |
|
|
Tetra-series 10_4_Powertower.pdf : the first conjecture about alternating series of powertowers of increasing height (06.2007)
10_4_Powertower_article.pdf : the same, but shorter, compacter and written more for a department journal.
In June, 2007 I had a discussion in the newsgroup sci.math.research, where I asked for crosscheck of my proposed method for summing the alternating iteration series for various bases b>e^-e , which seemed possible even for bases, where the powertower of infinite height is also infinite (bases b>e^(1/e)). It occurred a strong suggestion that the method is valid for the alternating series of powertowers of increasing heights. See here an edited version of that discussion : iterationseries discussion . |
|
|
Tetra-geometric-series Tetration_GS_short.pdf : the 2'nd conjecture; about alternating series of powertowers of like height |
|
|
Tetra-eta-series Tetra_Etaseries.pdf : a short treatise about alternating series of towers of like height, but different bases (like zeta() and eta() series) |
|
|
Various |
|
|
ProblemWithBellmatrix.pdf : In the computation of the Tetra-series we find an inconsistency for infinite series of negative heights. Here one attempt to identify and possibly resolve the problem by careful description of the Bell-matrix is discussed
|
|
|
Exploring_the_eigensystem.pdf : Considerations about the eigensystem of the tetration operator-matrix. Sketchy manuscript |
|
|
operators.pdf : a short treatise about a formulation for binary operators ("Add","Mul","Pow") adapted to the related matrix-expressions. |
|
Some work with summation
Summation.htm : Comparision of Euler-summation and Stirling-matrix based summation of zeta/eta-values
|
|
Literature
Here is a compilation of historical and contemporary literature, which I found interesting, most of it online available. For a much more extensive list see [Galidakis] below.
[EulerE489] De formulis exponentialibus replicatis
L. Euler
Acta Academiae Scientarum Imperialis Petropolitinae 1, 1778, pp. 38-60
http://math.dartmouth.edu/~euler/docs/originals/E489.pdf
[EulerE532] De serie Lambertina plurimisque eius
insignibus proprietatibus.
L. Euler
Acta Academiae Scientarum Imperialis Petropolitinae 1779, 1783, pp. 29-51
http://www.math.dartmouth.edu/~euler/pages/E532.html
[Eisenstein] Entwicklung von α ^ (α ^ (α ^ (α ^ ....))).
G. Eisenstein,
J. reine angev. Math. 28, pp 48-52, 1844.
http://www-gdz.sub.uni-goettingen.de/cgi-bin/digbib.cgi?PPN243919689_0028
[Schr] Über iterirte Funktionen
Ernst Schröder
in: Mathematische Annalen, Band 3, Heft 296, 1871
http://www.digizeitschriften.de/no_cache/home/jkdigitools/loader/?tx_jkDigiTools_pi1[IDDOC]=299680&tx_jkDigiTools_pi1[pp]=304
[Bak] Baker, Irvine Noel; Zusammensetzungen ganzer
Funktionen
1958; Mathematische Zeitschrift, Vol 69, Pg 121-163,
[EJ61] On analytic iteration;
Paul Erdös, Eri Jabotinsky
J. Anal. Math. 8, 361-376 (1961) (also
online at digicenter göttingen)
[Comtet] Advanced Combinatorics
Comtet, Louis
D. Reidel Publishing Company; Dordrecht, Holland; 1970.
pages 144-148
[Knuth] Mathematics
and Computer Science. Coping with Finiteness.
D. E. Knuth
Science 194, pp. 1235-1242, 1976.
[Knoebel] Exponentials
Reiterated
R. A. Knoebel
The American Mathematical Monthly, 88, pp. 235-252, 1981.
[Länger] An
elementary proof of the convergence of iterated exponentiations
H. Länger
Elem. Math. 51, pp. 75-77, 1986.
[WA91] Infinitely
Differentiable Generalized Logarithmic and Exponential Functions
Peter L. Walker
Mathematics of Computations, Vol.57, No. 196 (Oct., 1991), 723-733 (JStore)
[Bachmann] Convergence
of infinite exponentials
Gennady Bachman
Pacific Journal of Mathematics, Vol. 169, no. 2, 1995
http://projecteuclid.org/euclid.pjm/1102620323
[AF97] Continuous
iteration of dynamical maps
R. Aldrovandi and L.P.Freitas
Online at arXiv physics/9712026 16.dec 1997
[Berkolaiko] Analysis
of Carleman Representation of Analytical Recursions
G. Berkolaiko, S. Rabinovich and S. Havlin
Journal of Mathematical Analysis and Applications 224, 81-90 (1998)
http://www.math.tamu.edu/~berko/papers/pdf/jmaaBRH98.pdf
[Harrell] A
Short History of Operator Theory
Evans M. Harrell II
© 2004. Unrestricted use is permitted, with proper attribution, for noncommercial
purposes.
http://www.mathphysics.com/opthy/OpHistory.html
[Gralewicz] Continuous
time evolution from iterated maps and Carleman linearization
P.Gralewicz and K. Kowalski
Department of Theoretical Physics, University of Lódz, Poland
http://arxiv.org/PS_cache/math-ph/pdf/0002/0002044v1.pdf
[A&S] Handbook
of mathematical functions
Abramowitsch, M. and Stegun, I.A.;
9th printing
page 824; online at http://www.math.sfu.ca/~cbm/aands/
Further references can be found at:
[1] Wikipedia : "tetration", superlogarithm, iteration of functions, Bell/Carleman-matrix
[2] Andrew Robbins, "home of tetration" references in article
[3] Ioannis Galidakis, section "Lambert-W, tetration..." references
Links
[Galidakis] Ioannis
Galidakis, Tetration, LambertW-function
and more; online at
http://ioannis.virtualcomposer2000.com/math/
[Geisler] Daniel Geisler, Tetration-pages; online at
http://www.tetration.org
[McDonnell]
http://www.faculty.fairfield.edu/jmac/ther/tower.htm
[Robbins] Andrew Robbins, Tetration-pages, online at:
http://tetration.itgo.com/
[Weissstein] http://mathworld.wolfram.com/LambertW-Function.html
An extensive discussion is led at tetration-forum:
[TForum] Henryk Trappmann, Henryk Trappmann
et al. at: tetration-forum
Tetration-forum: thread “Bummer”
Tetration-forum: thread “inconsistency in using different fixpoints”
Andrew Robbins; Notations and Opinions; in "Tetration-forum" (2008)
http://math.eretrandre.org/tetrationforum/showthread.php?tid=114 (ff)
http://math.eretrandre.org/tetrationforum/showthread.php?tid=184
http://math.eretrandre.org/tetrationforum/showthread.php?tid=104&pid=979#pid979
http://math.eretrandre.org/tetrationforum/showthread.php?tid=114&pid=1692#pid1692
An older usenet-discussion
Iterated
exponentiation (tetration) to non-integral indices
Replies: 7 Last Post: Jul 13, 2000 6:16 PM
http://mathforum.org/kb/message.jspa?messageID=251709&tstart=0
Diagonalization and Eigendecomposition (online dictionaries)
http://mathworld.wolfram.com/MatrixDiagonalization.html
http://mathworld.wolfram.com/EigenDecomposition.html
Wikipedia:
http://en.wikipedia.org/wiki/Diagonalizable_matrix
http://en.wikipedia.org/wiki/Eigenvalue
http://en.wikipedia.org/wiki/Eigendecomposition_%28matrix%29
Andrew
Robbins and unknown authors; in: Wikipedia "Tetration"; 2008
http://en.wikipedia.org/wiki/Tetration
(unknown
authors); in: Wikipedia "Iterated function"; 2008
http://en.wikipedia.org/wiki/Iterated_function;
jan 2008
Divergent summation
[Vol] Volkov,
I.I.; Riesz summation method
Online reference Springer:Encyclopaedia of Mathematics
Edited by Michiel Hazewinkel
online at http://eom.springer.de/r/r082300.htm